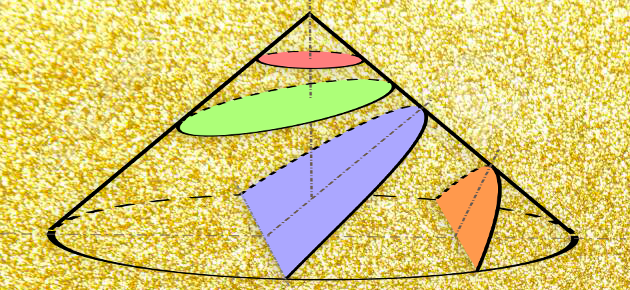
Avec la parabole et l’hyperbole, l’ellipse est l’une des trois coniques. D’abord examinées dans le cadre de la résolution de problèmes nécessitant des outils supplémentaires à la règle et au compas, comme la duplication du cube, elles sont ensuite unifiées par leur définition géométrique comme intersection d’un plan et d’un cône.
L’ellipse, qui semble n’être qu’un simple cercle aplati, présente des propriétés surprenantes, qu’il s’agisse du calcul de son périmètre, de différentes méthodes de construction qu’on peut lui imaginer ou des propriétés pratiques que sa définition bifocale permet, l’une d’elles étant la démonstration de l’héliocentrisme.