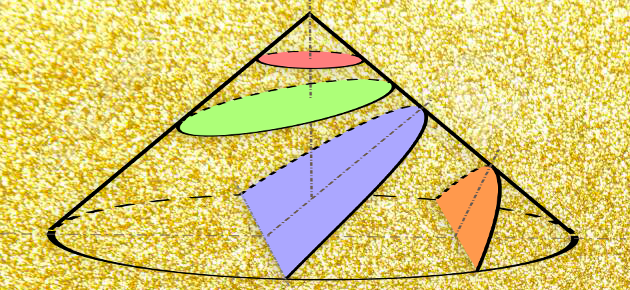
L’ellipse fait partie des trois coniques. Étrangement, son nom n’est pas construit sur le même modèle que ceux des deux autres, la parabole et l’hyperbole, qui présentent le suffixe « bole » (de ballô, « lancer » en grec). Ce qui pourrait sembler un point anecdotique de linguistique relève en réalité d’une spécificité mathématique notée par Apollonius de Pergé, l’inventeur des trois termes désignant les coniques.
Des sections aux courbes
S’ils ont singulièrement privilégié les constructions géométriques par règle et compas, les Grecs n’en ont pas moins utilisé d’autres courbes que la ligne circulaire et la ligne droite face à leurs problèmes (voir encadré).
La duplication du cube
Certains problèmes ne sont pas solubles à la règle et au compas. C’est le cas de la duplication du cube : à partir d’un cube donné de côté a, on cherche à construire un cube de volume double, soit 2a 3.
Dès le Ve siècle avant J.-C. un lien est fait avec l’obtention de deux moyennes proportionnelles enchainées : à partir de deux segments de longueurs a et 2a, on peut construire deux segments de longueurs x et y telles que
Cela nous donne x 3 = 2a 3, le volume recherché. Pour le déterminer, Ménechme (vers −380 ; ... Lire la suite
