Des ellipses aux superellipses

L’aire de la portion de plan située à l’intérieur d’une ellipse peut se calculer de plusieurs manières. On peut utiliser le calcul intégral (voir en page 32), mais il existe aussi une formule simple : A = πab, où a et b désignent le demi-grand axe et le demi-petit axe de l’ellipse. Lorsque a = b = r, on retrouve, bien sûr, l’aire du disque.

Le mathématicien suisse Jakob Steiner posa les deux problèmes suivants.

• De toutes les ellipses circonscrites à un triangle donné, quelle est celle dont l’aire est minimale ?

• De toutes les ellipses inscrites dans un triangle donné, quelle est celle dont l’aire est maximale ?

Jakob Steiner (1796-1863). 

Ces problèmes se résolvent facilement grâce aux propriétés des projections. En projetant un triangle quelconque sur un plan judicieusement choisi, il est toujours possible de faire en sorte que le triangle projeté soit équilatéral, quel que soit le triangle (non aplati) de départ. Or l’ellipse d’aire minimale circonscrite à un triangle équilatéral est un cercle, de même que l’ellipse d’aire maximale inscrite dans un triangle équilatéral. De plus, une projection, si elle ne conserve pas les aires, conserve en revanche le rapport entre les aires de deux figures.

Prenons comme exemple les ellipses circonscrite et inscrite dans un triangle 3-4-5 dont l’aire est de 6 unités.

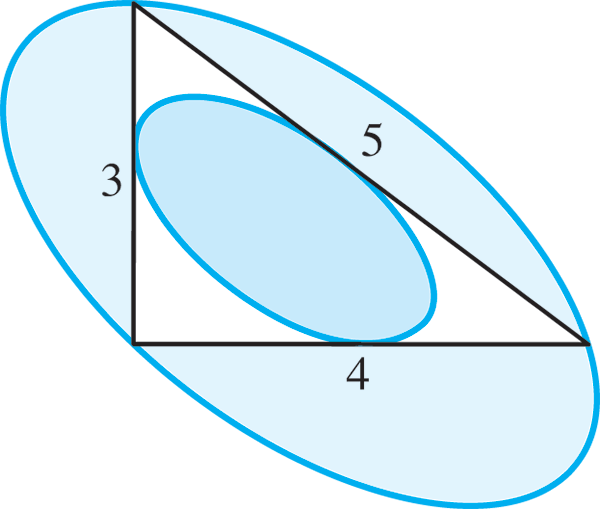
Le cercle inscrit dans un triangle équilatéral de côté c a pour rayon  le disque ayant pour aire πc²/12, et son cercle circonscrit a un rayon deux fois plus grand, l’aire du disque valant quant à elle le quadruple de celle du disque inscrit. 

En déduire les aires des régions du plan intérieures aux ellipses circonscrite et inscrite dans le triangle 3-4-5.

Les superellipses

Si vous tapez le mot « superellipse » dans un moteur de recherche, la première page qui vous sera proposée ne sera pas une page de mathématiques, mais une page consacrée à du mobilier. Ce mot a, en effet, été adopté par des designers, notamment du nord de l’Europe.

Piet Hein (1905-1996) est un physicien danois. Il est aussi poète, co-inventeur du jeu de Hex, créateur de nombreuses récréations mathématiques, et considéré par les designers comme un des leurs. 

Dans les années 1950, la ville suédoise de Stockholm décide de rénover un vieux quartier de la ville. Les architectes en charge du projet souhaitent construire le nouveau quartier autour d’une place de forme ovale. Ils s’adressent à Piet Hein pour lui demander conseil. Hein leur suggère de construire cette place en utilisant une courbe définie par une équation du type  avec n = 2,5, et il appelle de telles courbes des superellipses.

Sergels torg, la place de Stockholm aménagée selon les conseils de Piet Hein. 

Ces courbes étaient en fait connues depuis longtemps. Le mathématicien français Gabriel Lamé (1795-1870) les a décrites en 1818. 

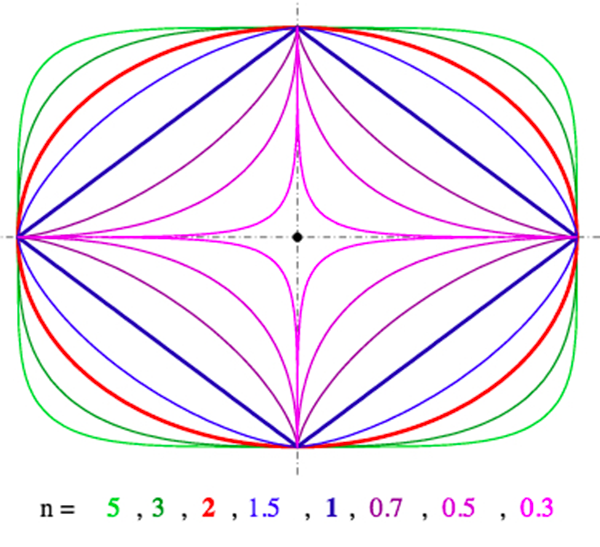
Lorsqu’on fait varier n de 2 vers l’infini, on se rapproche de plus en plus d’un rectangle. Dans l’autre sens, lorsque n varie de 2 vers 1, on se rapproche de plus en plus d’un losange, que l’on atteint pour n  = 1. Ensuite pour 0 < n < 1, les flancs de l’ellipse se creusent et l’aire intérieure de la courbe diminue jusqu’à disparaître.