Dessinons un cercle et un de ses diamètres, traçons plusieurs segments joignant perpendiculairement le diamètre au cercle et marquons les milieux de ces segments. Nous obtenons, par définition, une ellipse dont le rayon majeur (demi-grand axe) est le double du rayon mineur (demi-petit axe). De façon plus générale, si on projette un point M1 d’un cercle de rayon a = OA en un point H sur un de ses diamètres, alors l’ensemble des points M tels que est égal à une constante k < 1 est l’ellipse de rayon majeur a et de rayon mineur OB =b = ka.
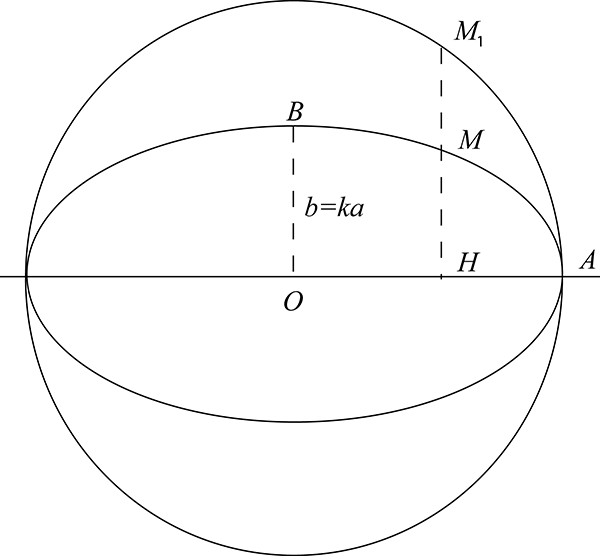
Nous avons ainsi effectué une affinité de rapport k. Ce qui est remarquable, c’est que si nous faisons de même avec une affinité de rapport 1/k appliquée à un petit cercle de rayon b, cercle que nous allongeons horizontalement au lieu de compresser verticalement le grand cercle, nous obtenons la même ellipse.
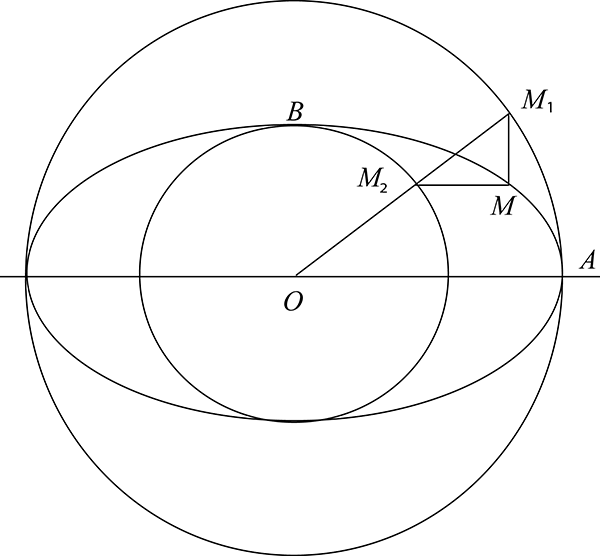
Conséquence notable : si nous traçons deux cercles concentriques de rayons a et b, nous pouvons obtenir grâce à la remarque précédente une construction point par point à la règle seule de l’ellipse, construction illustrée ci-dessous.