Inégalités en puzzles

En vertu de l’inégalité triangulaire, dans tout triangle non aplati, la somme des longueurs des deux plus petits côtés est strictement plus grande que la longueur du plus grand côté. Cette inégalité est évidemment vérifiée dans un triangle rectangle. Mais peut-on majorer la somme des longueurs des deux cathètes (les deux plus petits côtés) d’un triangle rectangle en fonction de la longueur de son hypoténuse (le plus grand côté) ?

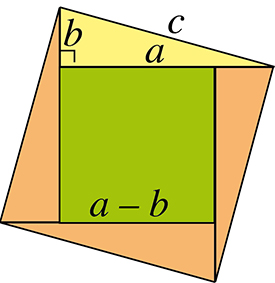
Le puzzle ci-dessus illustre bien le théorème de Pythagore. En effet, si a et b désignent les longueurs des cathètes du triangle jaune et c celle de son hypoténuse, on a c² = 2ab + (a – b)², soit c² = a² + b².

Complétons le puzzle à l’aide de quatre triangles identiques au triangle initial de façon à obtenir un grand carré de côté a + b.

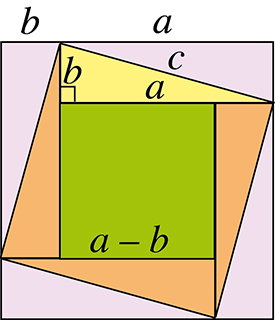
Lorsque le carré vert est visible (donc d’aire non nulle), on a (a + b)² < 2c², d’où a + b < c√2.

Imaginons maintenant que l’on fasse varier continûment la longueur du côté b (avec a qui reste constante). On obtient alors le « film » ci-dessous, dans lequel le carré vert (de côté a – b) va décroître, jusqu’à disparaître complètement, avant de réapparaître, puis de croître continûment.

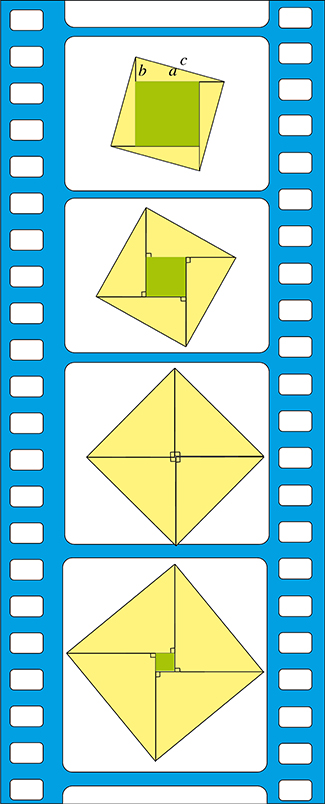
Lorsque le triangle rectangle initial est isocèle, le carré vert a disparu et on a alors l’égalité a + b = c √2. On peut donc affirmer que, dans tout triangle rectangle, on a c < a + b ≤ c √2.

Et avec d’autres triangles ?

Considérons maintenant des triangles ayant un angle de 120°. Soient c la longueur du côté opposé à l’angle de 120° (donc le plus grand côté du triangle) et a et b les longueurs des deux autres côtés.

Par une méthode analogue à la méthode utilisée dans le cas des triangles rectangles, montrez que, dans un triangle ayant un angle de 120°, on a l’inégalité a + b ≤ √6 × c/2. Dans quel cas a-t-on égalité ?