
Une parabole « en négatif »
Considérons une courbe plane, par exemple une parabole et construisons ses tangentes en une vingtaine de points également répartis.
On voit « apparaître » la courbe comme enveloppe de ses tangentes. On peut vérifier cette intuition en superposant les deux graphiques.
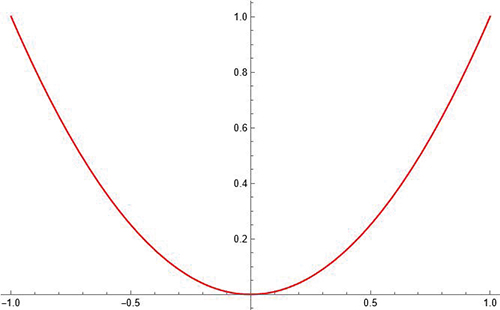
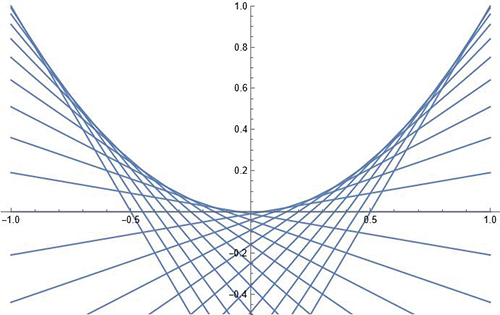
On pourrait croire que cela est vérifié parce que la parabole est une courbe « très simple »…
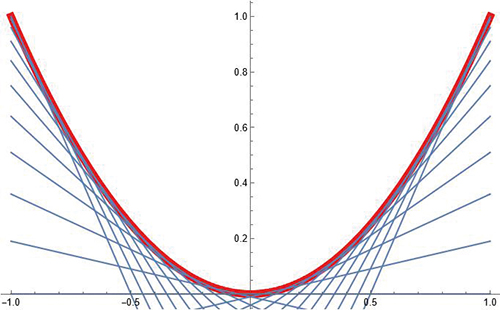
Les courbes définies par leurs tangentes
Il n’y a pas que la parabole que l’on voit « apparaître » comme enveloppe de ses tangentes (voir ci-dessus). Il s’agit en fait d’un phénomène assez général. Voyons une courbe plus élaborée.
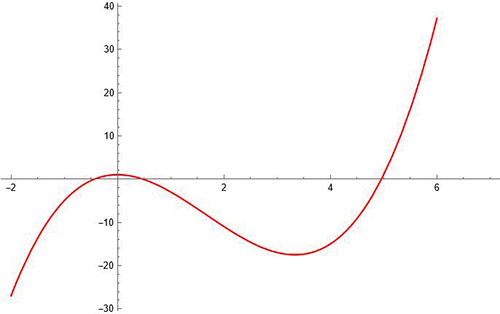
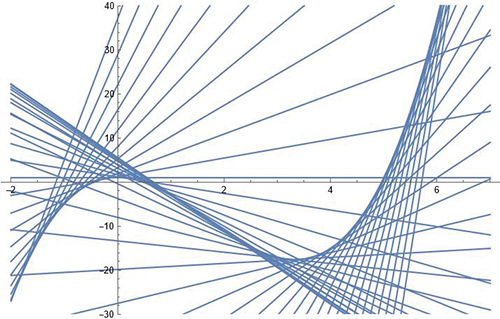
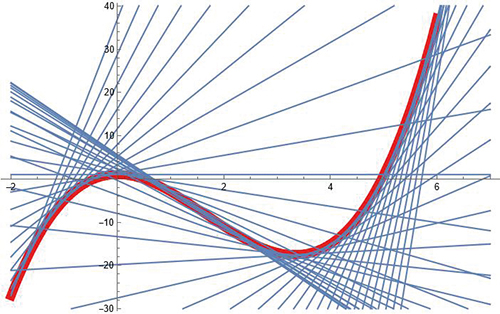
En fait, cela est vrai pour toute courbe « régulière » (en ce sens qu’en tout point, on peut définir une tangente) : une telle courbe est l’enveloppe de la famille de ses tangentes.
Inversement, étant donnée une famille de droites, peut-on trouver une courbe qui les admette toutes pour tangente ? Après différents travaux au cours du XVIIe siècle, c’est Leibniz qui en donne une réponse positive dans le cas où la famille est définie par un paramétrage de classe C1 (au sens où la dérivée partielle par rapport à ce paramétrage existe et est continue) !
Référence
Dossier ... Lire la suite gratuitement
