
Si, dans le plan euclidien muni d’un repère, on se donne une courbe (C) d’équation f (x) = 0, ainsi que deux points M0 et M de la courbe (d’abscisses respectives x0 et x), le coefficient directeur de la droite sécante (M0M) est donné par le taux de variations entre les points M0 et M : il est égal à .
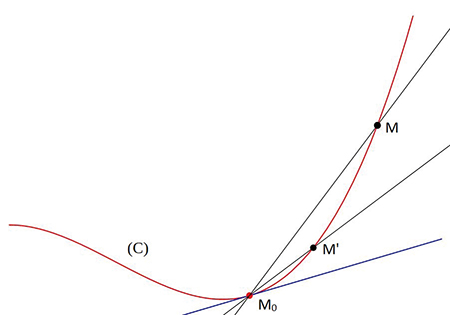
Quand le point M tend vers M0, la droite (M0M), sécante à la courbe (C), tend, en général, vers une position qui est celle de la tangente en M0 à (C) (en bleu dans le graphique) : même sans définir précisément cette notion de limite, on peut constater, sur le graphique, que la droite (M0M’) est « plus proche » de la tangente en M0 que la droite (M0M) car le point M’ est « plus proche » de M0 que M. Des cas particuliers peuvent se produire en certains points où il n’y aura pas de tangente ou pour des courbes très « pathologiques ».
Le coefficient directeur de la tangente est donc, en général, la limite du coefficient directeur de la droite (M0M), c’est-à-dire la limite du taux de variation entre M0 et M quand M tend vers M0, autrement dit quand x tend ... Lire la suite gratuitement
