
Le cas emblématique de l’hyperbole
La première rencontre avec une asymptote a généralement lieu au lycée, lors de l’étude de la fonction inverse, dont la courbe, d’équation dans un repère orthonormé, possède les deux axes du repère comme « asymptotes ».
Le point M de la courbe, de coordonnées se situe à la distance
de son projeté orthogonal H, de coordonnées (x, 0), sur l’axe des abscisses. Cette distance tend vers 0 lorsque x tend vers l’infini, mais sans jamais être égale à 0. Donc la courbe « se rapproche » de l’axe des x sans jamais l’atteindre.
Cette idée se trouve dans l’étymologie du mot « asymptote » : formé du préfixe privatif « a » et du grec symptôsis (« rencontre »), il signifie fondamentalement « pas de rencontre ».
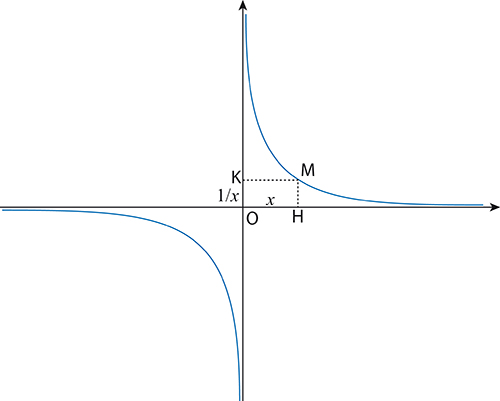
La courbe représentative de l’hyperbole.
Les courbes mathématiques sont sans épaisseur
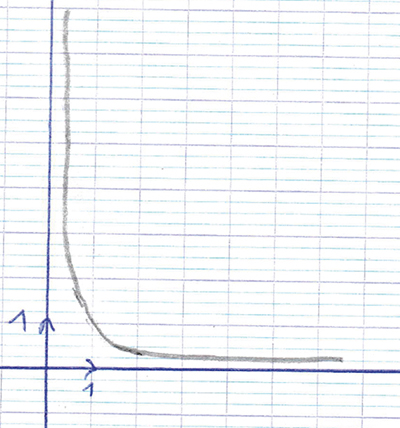
Parfois, lorsqu’on insiste sur le côté « pas de rencontre » entre une courbe et son asymptote (typiquement en contexte scolaire), le lycéen ou l’apprenant réalise spontanément une figure du type suivant.
À cause de l’épaisseur du trait de crayon, le tracé de la courbe vient en réalité se confondre avec celui de l’axe. Or, les courbes mathématiques sont des ... Lire la suite gratuitement
