Alpha, Beta et Epsilon ont décidé d’aller rendre visite à Tau, le grand frère d’Alpha, dont le cursus à l’X n l’a conduit à faire une halte sur Prepaterra. Il loge à Bourg-en-Braess (BB), une ville accessible en tradimobile depuis l’Institut intergalactique, ce qui représente une occasion en or pour Bêta d’étrenner son permis tout neuf. Les trois camarades ont prévu de partir dès la fin des cours, bien que cela implique de se retrouver en heure de pointe sur la route, en même temps que tous les employés de l’Institut qui, après leur journée de travail, rentrent à BB où se situe le lotissement qui leur est dédié.
« Il y a deux chemins possibles pour rejoindre Bourg-en-Braess, expose Bêta en examinant une carte. On peut soit passer par Simpson City, soit par Newcomb Village. »
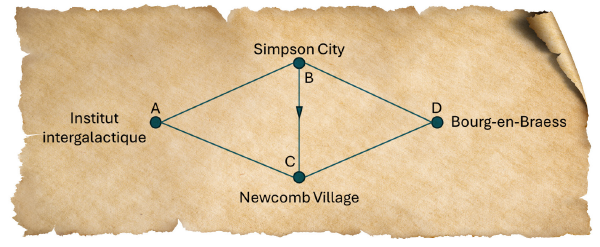
« On peut aussi passer par Simpson City et Newcomb Village, fait remarquer Alpha, en utilisant le nouveau télétransporteur à sens unique. Mais ça rallongerait le chemin…
‒ Pas sûre ! s’exclame Epsilon, qui s’est connectée sur une base de données recensant les durées de différents trajets. Le temps nécessaire pour aller de l’Institut à Simpson City dépend de la fréquentation de la route. Quand elle est vide, on ne met que trois minutes, mais quand elle est saturée, alors cela prend vingt minutes. Avec un taux d’occupation de la route de 50 %, on met sept minutes et trente secondes. On retrouve le même genre d’influence des bouchons sur la route qui mène de Newcomb Village à Bourg-en-Braess : deux minutes si l’on est tout seul, huit minutes trente secondes quand la route est saturée, et quatre minutes et trente secondes quand elle est fréquentée à 50 %. On pourrait modéliser ces temps de trajet par des équations du second degré avec le taux d’occupation du tronçon de route comme variable… En revanche, Newcomb Village est relié à l’Institut intergalactique par un télétransporteur de première génération qui implique un temps de trajet constant, pour tous les utilisateurs, de vingt-deux minutes. Entre Simpson City et Newcomb Village, le télétransporteur de nouvelle génération autorise un déplacement en trente secondes seulement. Enfin, entre Simpson City et Bourg-en-Braess, un large boulevard permet un déplacement en dix minutes quand la route est vide et en douze minutes lorsqu’elle est saturée. Une équation du premier degré en fonction du taux d’occupation permet de modéliser la durée du trajet. »
À partir de ces données, pourriez-vous modéliser les durées des trajets sur les différents tronçons en fonction de leur taux d’occupation ?
Des résultats contre-intuitifs
« Quel chemin vaut-il mieux prendre ? demande alors Bêta.
‒ Il suffit de comparer les durées des trajets possibles, répond Epsilon. Pour comparer
A‒B‒D et A‒B‒C‒D, il suffit de s’intéresser à B‒D et B‒C‒D, le premier tronçon étant commun. Et pour comparer A‒C‒D et A‒B‒C‒D, on regarde A‒C et A‒B‒C, puisque cette fois, c’est le dernier tronçon qui est identique. »
Elle s’empare de son calculateur et effectue rapidement quelques opérations. « On arrive à un résultat étonnant ! s’exclame-t-elle. Tous les tradimobilistes ont intérêt à prendre le même chemin… »
Cher lecteur, quel est-il et quelle est sa durée ?
Alpha fronce alors les sourcils. « Zut ! s’exclame-t-il, le téléporteur entre Simpson City et Newcomb Village est en panne depuis plusieurs semaines…
‒ On va mettre plus de temps à atteindre Bourg-en-Braess, du coup, grimace Bêta, avec un trajet possible en moins… »
Epsilon pianote à nouveau sur son calculateur. « Je pensais m’être trompée, finit-elle par déclarer d’un air surpris, mais le résultat est cette fois aussi plutôt contre-intuitif ! »
Avec le tronçon B‒C coupé et en supposant que les usagers se soient répartis de manière optimale entre les deux chemins restants, quelle est la nouvelle durée moyenne du trajet ?

