Le diamètre du cercle est constant, mais cette propriété ne lui est pas exclusive. Observez la « roue triangulaire » ci-contre. Cet objet convexe dans le plan, nommé triangle de Reuleaux, construit à partir de trois arcs de cercles centrés aux sommets opposés d'un triangle équilatéral, possède lui aussi un diamètre et une largeur constants.
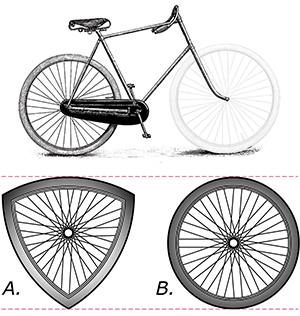
Ainsi, le périmètre de la roue A en forme de triangle est égal à la circonférence de la roue B ! Par conséquent, en pédalant le même nombre de tours, on devrait couvrir les mêmes distances. Le hic est d'imaginer un système mécanique qui permettrait à la roue A une conduite confortable et sans rebonds. La solution serait de fixer un disque à la fourche avec un canal coulissant circulaire.
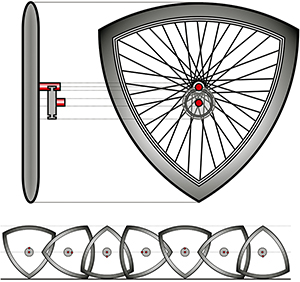
Un Chinois s'appelant Guan Baihua a justement passé dix-huit mois à construire une bicyclette qui roule avec un système analogue !


