En 1936, Soddy publie un article, dans la revue Nature Magazine, consacré à une question de géométrie (voir Mathématiques et Chimie, Bibliothèque Tangente 43, 2012). Le problème est le suivant : si trois cercles sont tangents extérieurement deux à deux, on peut toujours en trouver un quatrième qui soit tangent à ces trois cercles. Dans le cas général, on peut même en trouver deux, les trois cercles étant tangents extérieurement à l’une des solutions, et intérieurement à l’autre.
1. Dans quel cas n’a-t-on qu’une solution ?
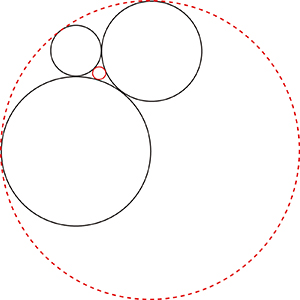
Quelle relation lie les rayons de quatre cercles tous tangents entre eux ? Une formule fut trouvée par Soddy. Si a, b et c désignent les rayons des trois cercles initiaux et r le rayon d’une des deux solutions, alors on a la relation suivante :

Cette relation avait déjà été formulée en 1643 par René Descartes dans une lettre adressée à la princesse Élisabeth de Bohème.
L’originalité de l’article de Soddy est qu’il n’a pas été rédigé comme un texte mathématique, mais sous la forme d’un poème, intitulé The Kiss Precise (« Le baiser précis »), en trois strophes de huit vers. La deuxième strophe, ci-dessous, suivie de la traduction de Claude Roux, dans Nouveaux Divertissements mathématiques (Martin Gardner, Dunod, 1970), énonce la propriété.
« Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance from the center.
Though their intrigue left Euclid dumb
There’s now no need for rule of thumb.
Since zero bend’s a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum. »
« Quatre cercles viennent s’embrasser.
Le plus petit étant le plus courbé.
La courbure est juste l’inverse
De la distance au centre.
Bien que cette intrigue ait laissé Euclide muet
Nous n’avons plus besoin de règles empiriques.
Comme une courbure nulle est celle d’une ligne droite
Et qu’une courbure concave a un signe moins,
La somme des carrés des quatre courbures
Est égale à la moitié du carré de leur somme. »
2. En supposant que les trois cercles initiaux aient pour rayons respectifs 1 cm, 2 cm et 3 cm, quels seraient les rayons des deux cercles rouges ?

