
Le principe du flexagone a été introduit en 1939 par le mathématicien britannique Arthur Harold Stone, spécialiste de topologie. L’histoire raconte qu’étudiant à Princeton, dans le New Jersey (États-Unis), il découpait un bord de ses copies au format européen A4 (21 cm × 29,7 cm) pour les insérer dans un classeur au format américain letter (21,5 cm × 27,9 cm). Au lieu de jeter ces bandes de papier, il les utilisait pour réaliser des pliages et c’est ainsi qu’il aurait créé les premiers flexagones, qu’il étudia ensuite avec un groupe d’amis : le mathématicien Bryant Tuckerman, le légendaire physicien Richard Feynman et le statisticien John Tukey.
Ciseaux, colle, et un peu de patience
En théorie, il existe une infinité de flexagones. Commençons par le plus simple : le trihexaflexagone. Pour construire cet objet, dessinez ou photocopiez cette bande, si possible sur un papier suffisamment épais et en augmentant ses dimensions.
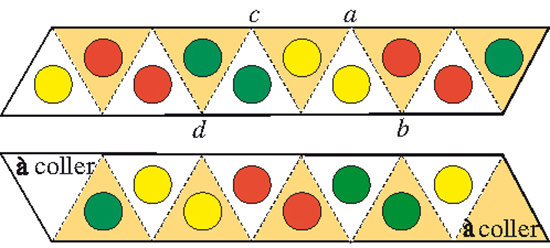
Les deux faces de la bande de papier, avec une éventuelle décoration à adapter selon votre inspiration.

Une fois collé, le flexagone est une surface à une seule face et un seul bord (une bande de Möbius), composée de dix-huit triangles équilatéraux.
Lorsque le flexagone est plié et aplati de façon à former un hexagone, six de ces triangles apparaissent d’un côté de l’hexagone et six autres de l’autre côté. Il reste donc six triangles « cachés » à l’intérieur du pliage, que l’on peut faire apparaître ou disparaître en « faisant flexer » le flexagone.
Les groupes entrent en jeu
L’opération est délicate et demande un peu d’entraînement. Le flexagone aplati présente sur chaque face trois losanges d’un seul morceau constitués de deux triangles juxtaposés. Le « flexage » consiste à placer l’un sur l’autre les triangles adjacents d’un même losange, puis à ouvrir la face arrière, en faisant apparaître les triangles cachés et disparaître ceux qui étaient visibles sur la première face.

Le film des transformations du trihexaflexagone.
On peut associer à cet objet mathématique une structure de groupe. Il s’agit d’un groupe de symétrie isomorphe au groupe des symétries d’un ennéagone régulier (polygone à neuf côtés).
En augmentant le nombre de triangles, on obtient des flexagones permettant de montrer davantage de « faces » différentes. Si le trihexaflexagone, constitué d’une bande de dix-huit triangles, ne permet de montrer que trois faces différentes, en portant le nombre de triangles à 24 (douze triangles d’un côté et douze de l’autre) on obtient un tétrahexaflexagone, qui présente quatre faces différentes.
En portant le nombre de triangles à 36 (dix-huit triangles visibles de chaque côté), on construit un hexahexaflexagone, qui présente six faces différentes.
Avec des carrés
Mais on peut aussi construire des flexagones à faces carrées, des tétraflexagones. Voici le modèle le plus simple, l’hexatétraflexagone, qui, contrairement à l’objet précédent, ne correspond pas à une bande de Möbius.
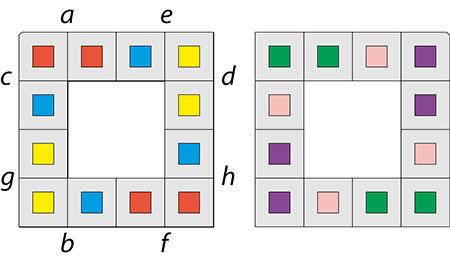
Les deux faces du flexagone déplié.
Pour construire ce flexagone, on plie d’abord selon (ab), puis selon (cd), puis selon (ef). Le dernier pli, selon (gh), est plus délicat car il faut rentrer le petit carré du coin dans le pli.
On obtient alors (souvent après plusieurs essais infructueux) le résultat suivant.
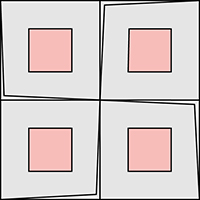
Nous vous laissons découvrir les différentes faces de ce flexagone. Ces curieux objets géométriques ont été popularisés par Martin Gardner dans sa chronique du Scientific American de décembre 1956.

