
Classer des mots
A priori, tout le monde sait utiliser un dictionnaire, et donc classer les mots. Mais la méthode de classement est-elle facile à expliquer ?
Le principe consiste à comparer les mots caractère par caractère. Si les premiers caractères sont identiques, on passe aux suivants. Si, ensuite, un caractère diffère, l’ordre entre les deux mots est connu.
Au-delà de la dernière lettre de l’un des deux mots, si toutes les lettres précédentes étaient identiques, le mot le plus court est considéré comme étant classé en premier. On écrira « < » entre deux mots pour dire que le premier se trouve avant le deuxième dans le dictionnaire. Ainsi, on a allo < amen < amendement < banc.
Cela paraît simple.
Mais que se passe-t-il quand il y a des accents, ou des signes diacritiques (lesquels modifient la prononciation d’une lettre) ? Dans la langue française, les lettres concernées sont à, â, ä, é, è, ê, ë, ï, î, ô, ö, ù, û, ü, ÿ et ç ! Il existe une règle spécifique : le classement ne doit pas tenir compte des signes diacritiques.
Ainsi, on leader < lécher < leçon < lecteur.
Mais comment classer si les deux mots ne diffèrent que par des signes diacritiques, auquel cas la règle précédente ne permet pas de conclure !
Alors, seule la première lettre (en partant de la gauche) pour laquelle il existe une différence sera prise en compte ; le mot placé en premier est celui où cette lettre est la plus « petite » en utilisant les deux conventions suivantes :
1. pas d’accent < accent aigu < accent grave < accent circonflexe < tréma ;
2. pas de cédille < cédille.
Ainsi, on a : chasse < chassé < châsse.
Enfin, en présence de mots composés séparés par une division (un trait d’union, comme dans après-midi) ou par une espace (comme dans a priori), on fait comme si les deux composantes étaient accolées. Ainsi : âpre < après-midi < a priori < à-propos < apte.
Classer des points ?
Peut-on classer les points du plan ? La réponse est oui. Une fois un repère défini, les points du plan sont déterminés par un couple de coordonnées. Le point M(x, y) est « avant » le point M’(x’, y’) si on a la relation x < x’ ou (x = x’ et y ≤ y’). Dans ce cas, on notera M ⟨⟨ M'. En fait, cette relation, appelée ordre lexicographique, ressemble à l’ordre du dictionnaire (voir § ci-dessus), mais en plus simple : il n’y a que deux nombres à comparer et ils sont plus « simples » que les lettres avec tous les signes diacritiques possibles !
Sur le graphique ci-dessous, où I est le point de coordonnées (1, 1), les points M vérifiant I ⟨⟨ M sont en rouge. Ce sont tous les points d’abscisse strictement supérieure à 1 ainsi que les points de coordonnées (1, y) avec y ≥ 1.
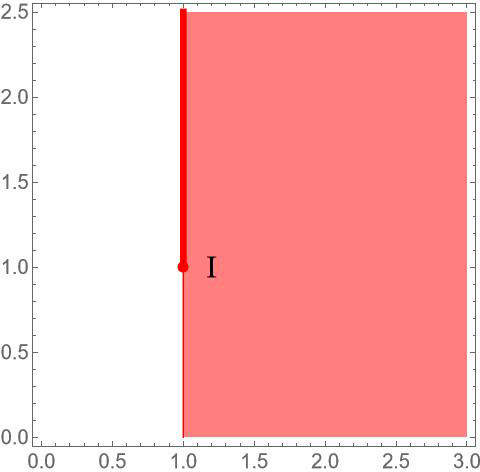
Cette relation ⟨⟨ est, bien sûr, une relation d’ordre total : deux points A et B quelconques sont toujours comparables (soit A ⟨⟨ B, soit B ⟨⟨ A, le cas A = B vérifiant bien sûr les deux relations, réflexivité oblige !).
Une autre manière de classer les points
La relation d’ordre ⟨⟨ (voir la brève ci-dessus) est-elle la seule possible dans le plan euclidien ? Non, bien sûr !
Par exemple, le plan, étant toujours défini comme ℝ2, on peut considérer l’ordre produit, noté ici ∠ : M(x, y) ∠ M’(x’, y’) si, et seulement si, x ≤ x’ et y ≤ y’.
Sur le graphique, où I est le point de coordonnées (1, 1), les points M vérifiant I ∠ M sont en rouge. Ce sont tous les points d’abscisse et d’ordonnée supérieures ou égales à 1.
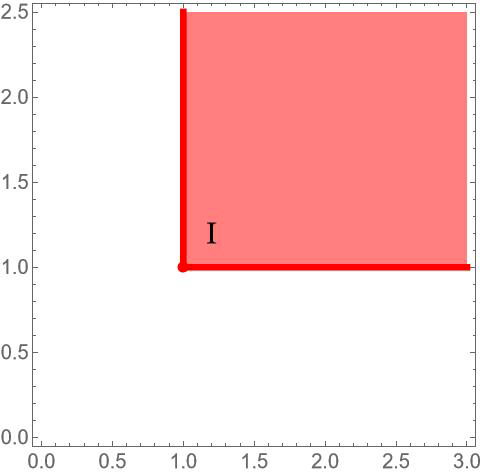
La relation binaire ∠ définit, bien sûr, une relation d’ordre… mais cet ordre n’est pas total ! Tous les points ne sont en effet pas toujours comparables au sens de ∠, par exemple les points de coordonnées (1, 2) et (2, 1).
On peut de fait imaginer une multitude de relations d’ordre entre les points du plan.


