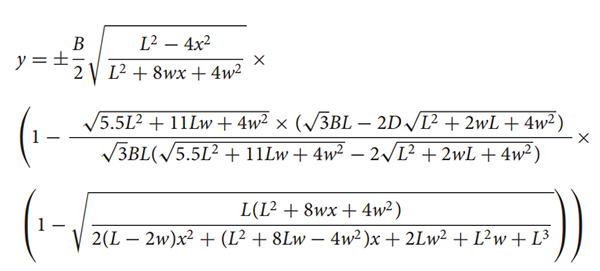Ils y incluent des éléments liés à quatre formes géométriques : sphère, ellipsoïde, ovoïde et piriforme (conique ou en forme de poire). Cette dernière, la moins célèbre, est obtenue en deux dimensions par la courbe paramétrée suivante : t → (cos2t ; cos3 t × sin t ) pour t ∈ [0 ; π].
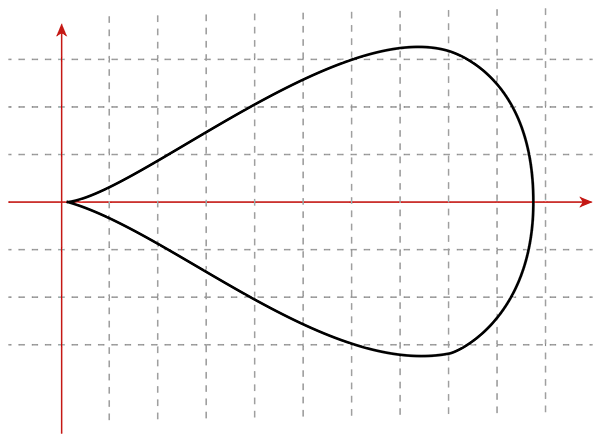
Ce problème de modélisation est plus important qu’il n’y paraît, car la forme de l’œuf, en fonction des espèces notamment, a un impact sur la survie de l’embryon (la forme a des conséquences sur la résistance) et permet donc d’approcher mathématiquement cette question sur le plan de l’évolution.
Le modèle permet de nombreuses applications pratiques en biologie aviaire (détection des parasites, identification du sexe in ovo, amélioration de l’éclosion…), mais relance également la réflexion théorique sur la nature mathématique de l’univers.