
Le voyage pourrait être très long, tant le nombre des inégalités mathématiques célèbres et utiles est grand. Ainsi, même en nous limitant aux plus « simples », on rencontre déjà des « vedettes », des inégalités puissantes et importantes.
A comme inégalité d’Aristarque
Si α et β sont les mesures de deux angles aigus, mesurés en degrés ou en radians, et si β < α, on a :
Elle porte le nom de l’astronome grec Aristarque de Samos qui pensait, dix-sept siècles avant Copernic, que les planètes tournaient autour du Soleil.

Aristarque de Samos (vers ‒310 ; vers ‒230), tel que représenté dans
Harmonia Macrocosmica d’Andreas Cellarius (1660).
AF comme inégalité des accroissements finis
L’un des théorèmes fondamentaux du calcul différentiel pour les fonctions à valeurs dans est le théorème des accroissements finis. Il généralise le théorème de Rolle, démontré en 1691 par Michel Rolle (1652‒1719). Voici son énoncé : si une fonction f est définie sur un intervalle [a, b] (avec a < b) à valeurs dans
, et si elle est continue sur [a, b] et dérivable sur ]a, b[, alors il existe c appartenant à ]a, b[ tel que f (b) ‒ f (a) = (b ‒ a) f’(c).
Sous cette forme moderne, il a été démontré en 1823 par Augustin-Louis Cauchy (1789‒1857). Ce théorème peut s’écrire sous la forme d’une inégalité. En effet, si f est continue sur [a, b] et dérivable sur ]a, b[ et s’il existe une constante M ≥ 0 telle que | f’(t) | ≤ M pour tout t appartenant à ]a, b[, alors on a l’inégalité des accroissements finis :
| f (b) ‒ f (a) | ≤ (b ‒ a) × M.
Le théorème des accroissements finis ne se généralise pas pour les fonctions vectorielles, c’est-à-dire à valeurs dans (avec n ≥ 2). Par contre, l’inégalité des accroissements finis, elle, se généralise et ce seul résultat est bien suffisant dans la plupart des applications.
Bern comme inégalité de Bernoulli
Elle exprime que, pour tout entier n strictement supérieur à 1 et tout réel x supérieur ou égal à ‒1, on a la relation (1 + x)n ≥ 1 + nx.
Énoncée en 1689 par Jacques Bernoulli (1654‒1705) à propos d’un calcul d’intérêts, elle a sans doute été établie précédemment. Elle se démontre par récurrence sur n. En effet, l’inégalité est vraie pour n = 2 : (1 + x)2 = 1 + 2x + x2 ≥ 1+2x car x2 ≥ 0. Supposons qu’elle soit vraie pour n fixé ; on a donc (1 + x)n ≥ 1 + nx.
Or (1+x)n+1 = (1+x)n(1 + x) ≥ (1 + nx)(1 + x) d’après l’hypothèse de récurrence ; puis, en développant :
(1 + x)n+1 ≥ 1 + (n + 1)x + nx2 ≥ 1 + (n + 1)x car nx2 ≥ 0. Le résultat est donc vrai au rang n + 1. D’après le théorème de récurrence, il est donc vrai pour tout n.
Cette inégalité se généralise en remplaçant l’entier n par le réel r vérifiant une relation analogue : r ≥ 1. Il y a alors besoin du calcul différentiel pour démontrer cette nouvelle inégalité.
Berns comme inégalité de Bernstein
Elle concerne les polynômes définis sur les nombres complexes et leurs dérivées. Si P est un polynôme complexe de degré inférieur ou égal à n et si k est un entier, on a :
Les valeurs maximales sont prises sur l’ensemble des nombres complexes de module inférieur ou égal à 1. L’égalité est réalisée avec le polynôme P(z) = azn. Cette inégalité a été obtenue dans les années 1910 par Sergueï Natanovitch Bernstein (1880‒1968) lors de ses travaux en théorie de l’approximation.
CS comme inégalité de Cauchy‒Schwarz
Démontrée initialement par Cauchy et publiée en 1821, elle concerne des réels, x1, x2… et xn d’une part, et y1, y2… et yn d’autre part. On a :
Elle sera ensuite généralisée à des intégrales par le Russe Victor Iakovlevitch Bouniakowsky (1804‒1889) et l’Allemand Hermann Amandus Schwarz (1843‒1921) ; voir article « L'inégalité de Cauchy-Schwarz ».
E comme inégalité d’Euler
Si on note r et R les rayons respectifs du cercle inscrit et du cercle circonscrit, on a 2r ≤ R. Cette inégalité porte le nom de Leonhard Euler (1707‒1783), qui l’a publiée en 1765. Néanmoins, elle avait été publiée avant. Elle devient une égalité quand le triangle est équilatéral.
FM comme inégalité des frères Markov
Non, ce ne sont pas les Marx Brothers, bien connus des cinéphiles, mais les « Markov brothers », plus précisément Andreï Andreïevitch (1856-1922) et son frère Vladimir Andreïevitch (1871‒1897), tous deux mathématiciens russes, le premier plus connu pour ses travaux sur les processus stochastiques, aboutissant à la notion qui s’appelle maintenant chaîne de Markov. L’inégalité qui porte leur nom concerne les polynômes et leurs dérivées. Si P est un polynôme réel de degré inférieur ou égal à n et si k est un entier, on a :
Dans les années 1890, Andreï a démontré l’inégalité pour k = 1 et c’est Vladimir qui l’a généralisée pour tout entier k. L’égalité est atteinte quand P est un polynôme de Tchebychev. Cette inégalité n’est pas contradictoire avec l’inégalité de Bernstein (voir plus haut) car les valeurs maximales sont prises ici sur l’intervalle réel [‒1, 1] et non sur le disque unité du plan complexe.
H comme inégalité de Hölder
Cette inégalité a été découverte en 1888 sous une forme légèrement différente par le Britannique Leonard James Rogers (1862‒1933), mais son nom lui a été donné en l’honneur d’Otto Ludwig Hölder (1859‒1937), qui en a donné une autre démonstration et l’a publiée en 1889.
Si x1, x2… xn et y1, y2… yn sont des réels et si p et q sont des réels strictement supérieurs à 1 tels que alors :
C’est une généralisation de l’inégalité de Cauchy‒Schwarz, que l’on retrouve en prenant p = q = 2. Il existe aussi une version avec des séries et différentes versions avec des intégrales. Par exemple : si f et g sont des fonctions intégrables sur l’intervalle [a, b] et si p et q sont des réels strictement
plus grands que 1 tels que alors :
HH comme inégalité d’Hermite‒Hadamard
Si une fonction f est convexe sur l’intervalle [a, b], elle y est intégrable (au sens de Lebesgue) et son intégrale vérifie les inégalités
Cette inégalité a été découverte en 1883 par Charles Hermite (1822‒1901), et a été prouvée de manière indépendante dix années plus tard par Jacques Hadamard (1865‒1963). C’est une des inégalités de base liée à la convexité. Elle a une interprétation graphique évidente : le premier terme de l’inégalité est l’aire du trapèze ACDB, l’intégrale est égale à l’aire du domaine en rouge et le dernier terme est l’aire du trapèze AEFB.
.jpg)
I comme inégalité isopérimétrique
Le problème, posé dès le IXe siècle avant notre ère, consiste à trouver une inégalité entre l’aire intérieure à une courbe fermée et son périmètre, puis de trouver la courbe fermée ayant la plus grande aire pour le plus petit périmètre. Si Δ est l’aire intérieure à la courbe et p son périmètre, on a :
p2 ≥ 4πΔ.
Le cas d’égalité est réalisé pour un cercle (voir article « Le problème de Didon »).
I.A.G. comme inégalité arithmético-géométrique
Cette inégalité porte sur les moyennes arithmétique et géométrique de n réels, x1, x2… et xn positifs ou nuls. Elle s’énonce simplement (voir article « Une histoire de moyennes bien rangées ») par :
Je comme inégalité de Jensen
Cette inégalité est liée à la notion de fonction convexe (voir page 18). Si f est une fonction convexe sur un intervalle I, si x1, x2… xn sont des réels appartenant à I et si λ1, λ2… λn sont des réels positifs tels que λ1 + λ2 + … + λn = 1, alors :
f (λ1x1 + λ2x2 + … + λnxn) ≤ λ1 f (x1) + λ2 f (x2) + … + λnf (xn).
Elle a été démontrée en 1906 par l’ingénieur danois Johan Ludwig William Valdemar Jensen (1859‒1925), mathématicien à ses heures, en s’appuyant sur un travail d’Otto Hölder. Comme pour beaucoup d’autres inégalités, il en existe une version avec des intégrales.
Jo comme inégalité de Jordan
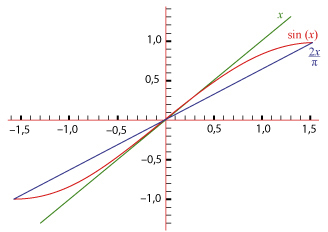
Elle doit son nom au français Camille Jordan et se visualise très bien. En effet, pour x inférieur (en valeur absolue) à π/2, on a :

Marie Ennemond Camille Jordan (1838‒1922).
M comme inégalité de Minkowski
Comme l’inégalité de Hölder, elle porte sur des réels et se généralise avec des séries ou des intégrales. Si x1, x2… xn et y1, y2… yn sont des réels et si p est un réel supérieur ou égal à 1, alors on a :
Pour p = 1, c’est une conséquence de l’inégalité triangulaire et pour p > 1 de la convexité de la fonction qui, à x ≥ 0, associe xp ainsi que de l’inégalité de Hölder.
Elle est nommée en l’honneur du mathématicien allemand Hermann Minkowski (1864‒1909), connu pour ses travaux en géométrie des nombres, sur la convexité et sur l’espace-temps (l’espace à quatre dimensions, support de la relativité générale développée par Albert Einstein).
S comme inégalité de Schur
Si x, y et z sont des réels positifs ou nuls et si r est un réel strictement positif, on a :
xr(x ‒ y)(x ‒ z) + yr(y ‒ x)(y ‒ z) + zr(z ‒ x)(z ‒ y) ≥ 0.
Elle porte le nom du mathématicien russe Issai Schur (1875‒1941), qui a laissé son nom sur quantité de résultats en mathématiques.
Tch comme inégalité de Tchebychev
Considérons les réels x1, x2… xn et y1, y2… yn tels que x1 ≥ x2 ≥ … ≥ xn et y1 ≥ y2 ≥ … ≥ yn. Alors on a :
Selon que les réels x1, x2… xn et y1, y2… yn forment des chaînes croissantes ou décroissantes, il existe d’autres inégalités (voir article « Tchebychev et les suites monotones »). À ne pas confondre avec l’inégalité de Bienaymé‒Tchebychev (voir aussi article « En probabilités : l'inégalité de Bienaymé-Tchebychev »).
Tri comme inégalité triangulaire
Sans doute la reine des inégalités ! Apparue dans les Éléments d’Euclide, vers ‒300, elle indique que, dans un triangle ABC, la longueur d’un côté est inférieure ou égale à la somme des longueurs des deux autres côtés : AC ≤ AB + BC (voir page 10). Exprimé avec le langage de tous les jours : le plus court chemin entre deux points est la ligne droite !
Cette inégalité est à la base de la notion mathématique de distance (voir Les Distances, Bibliothèque Tangente 81, 2023).
We comme inégalité de Weitzenböck
Dans un triangle où les côtés ont pour longueur a, b et c et où l’aire est notée Δ, on a :
Elle porte le nom du mathématicien autrichien Roland Weitzenböck (1885‒1955).
On rappelle qu’en vertu de la formule démontrée par le Grec Héron d’Alexandrie, ayant vécu au Ier siècle, l’aire Δ du triangle est égale à où p est le demi-périmètre du triangle, soit p = (a + b + c) / 2.
Wi comme inégalité de Wirtinger
Elle fait intervenir des intégrales, comme l’une des formes de l’inégalité de Cauchy‒Schwarz ou l’inégalité de Jensen, mais elle est sans doute un peu moins connue. Démontrée par le mathématicien autrichien Wilhelm Wirtinger (1865‒1945), elle possède plusieurs formes, dont on montre qu’elles sont équivalentes. Sous certaines hypothèses, elle établit une relation entre l’intégrale du carré d’une fonction et l’intégrale du carré de sa dérivée.
Si une fonction f est définie sur un intervalle [a, b] (avec a < b) à valeurs dans R, si elle est de classe C1 sur [a, b] (c’est-à-dire continue, dérivable et dont la dérivée est continue) et si f (a) = f (b) = 0, alors on a l’inégalité suivante :
Y comme inégalité de Young
La forme la plus simple de cette inégalité porte sur des nombres réels : elle indique que, si x et y sont des réels positifs ou nuls et si p et q sont des réels strictement plus grands que 1 tels que alors on a
Elle a été démontrée par le mathématicien britannique William Henry Young (1863‒1942), à qui l’on doit aussi le théorème de Taylor‒Young, généralisant le théorème des accroissements finis. Plusieurs démonstrations existent, l’une utilisant l’inégalité de Jensen. Cette inégalité, elle aussi, se généralise dans une version utilisant des intégrales.
