
Elle enseigne aujourd’hui dans le nord de l’Essex, dans l’équivalent d’un collège-lycée français, auprès d’élèves âgés de 11 à 18 ans. Depuis l’été 2018, elle publie sur le réseau social Twitter des « puzzles » géométriques, des petits dessins colorés réalisés à la main présentant une énigme géométrique. Ces petites enluminures aux couleurs vives et chatoyantes n’ont rien à envier aux célèbres sangaku japonais de l’époque Wasan (voir article « La belle géométrie des sangaku »), ni aux six premiers livres des Éléments d’Euclide revisités par Oliver Byrne en 1847 (Taschen, 2022 pour la dernière édition).
Souvent accompagnées d’une question demandant de calculer une aire ou un angle, les figures de Catriona Agg ne présentent que très peu de données, ce qui intrigue souvent au premier abord… et concourt à l’élégance des énigmes proposées.
L’engouement sur la Toile a été immédiat : beaucoup de personnes ont suivi assidûment les publications de la jeune enseignante à travers le monde entier, chacun y allant de sa solution, de sa remarque, de sa nouvelle suggestion, de sa généralisation. L’imagination de Catriona Agg semble sans limite ! Un petit livre disponible à la vente regroupe ses premières productions (Geometry Puzzles in Felt Tip, soit « Puzzles géométriques au feutre », Independently Published, 2019).
Un intérêt pédagogique majeur
Quand on demande à Catriona Agg pourquoi elle s’est lancée dans la réalisation de ses puzzles, elle répond tout d’abord en mentionnant son amour de la géométrie, du coloriage et surtout la nature visuelle des énigmes. Elle dit avoir la tête pleine d’images et aime expliquer les choses avec des diagrammes. Elle apprécie notamment l’aspect engageant de ces petits problèmes, leur aspect plus attractif, moins « mathématique » qu’une question d’algèbre.
Les activités construites autour de ces charmants dessins permettent de véhiculer auprès de ses plus jeunes élèves quelques principes fondamentaux : tout le monde peut s’améliorer en maths en apprenant de ses erreurs, les idées réfléchies valent plus que les réponses rapides, et bien penser consiste à se poser beaucoup de questions. Car le but de l’enseignante est bien de partir d’une image pour susciter des questions, chercher des généralisations ou des invariants. Évidemment, le recours à l’algèbre est souvent très efficace, mais pas toujours nécessaire : même les plus jeunes peuvent résoudre certains problèmes « en rusant », en regardant la figure sous un autre angle, en la redécoupant… Des résultats non triviaux se cachent derrière les figures les plus simples et leur découverte suscite la surprise et la joie.
Nul doute que les élèves et le public de Catriona Agg ne peuvent que profiter de son sourire et de son enthousiasme communicatif pour les mathématiques !
À vos crayons !
Comme dans les sangaku japonais, on trouve souvent dans les énigmes de Catriona Agg des cercles tangents les uns aux autres. Voici pour vous amuser quelques exemples mettant aussi bien en évidence la portée mathématique que la portée artistique de son œuvre !

Cinq cercles sont dans un carré.
L’aire des deux rouges vaut 24.
Combien vaut l’aire des trois cercles orange ?
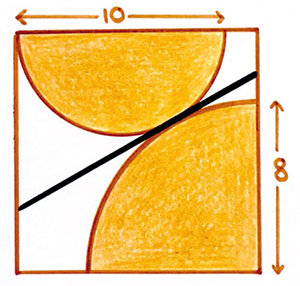
Un demi-cercle et un quart de cercle
se trouvent dans le carré.
Quelle est la longueur du segment en noir ?
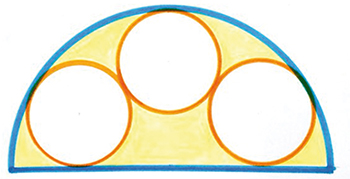
Quelle fraction de ce demi-cercle n’est pas couverte par les trois disques blancs (qui sont de même diamètre) ?
