
Une question d’intersection
La définition la plus simple de la tangence en géométrie se fait à l’aide d’un cercle et d’une droite. Dans le plan euclidien usuel, une droite (D) et un cercle ( ) peuvent avoir deux, un ou aucun point d’intersection. Dans le cas d’un point unique, on dit qu’ils sont tangents. En notant P ce point et O le centre du cercle, la droite (OP) est perpendiculaire à (D).
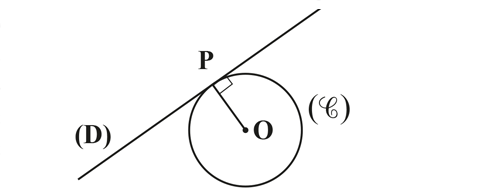
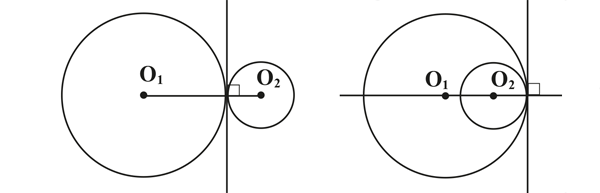
Deux cercles sont tangents (entre eux) s’ils sont tangents à la même droite (D) au même point. La droite reliant leurs deux centres est perpendiculaire à (D).
Considérons deux droites sécantes. Un cercle tangent à ces deux droites aura son centre sur une des bissectrices de ces deux droites et ses deux points de contacts seront à égale distance de l’intersection des deux droites.
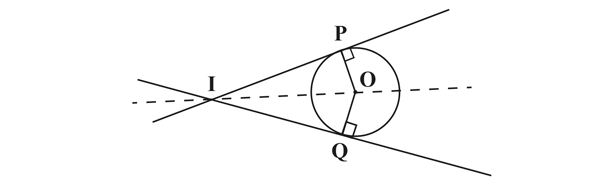
Les triangles rectangles OPI et OQI ont deux côtés de même longueur. La longueur des troisièmes côtés est donc égale, elle aussi ; on a ainsi IP = IQ. Par suite, les deux triangles étant semblables, les angles et
sont égaux.
Le cercle inscrit, tangent aux trois côtés d’un triangle
Trois droites non concourantes et non parallèles deux à deux forment un triangle. Les trois bissectrices (intérieures) de ce triangle sont concourantes et, d’après ce qui a été dit plus haut, ce point d’intersection est le centre d’un cercle tangent simultanément aux trois côtés du triangle : c’est le cercle inscrit dans ce triangle.
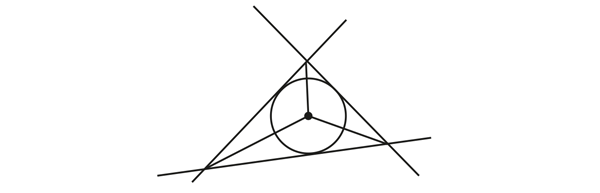
Lorsqu’il est rectangle, une jolie formule relie le rayon du cercle inscrit aux longueurs des côtés du triangle.
En effet, on a la relation suivante :
c = AR + BR = AQ + BP = (b ‒ r) + (a ‒ r), d’où l’on déduit 2r = a + b – c (on notera ici a (respectivement b, c) la longueur du côté opposé au sommet A (respectivement B, C)).
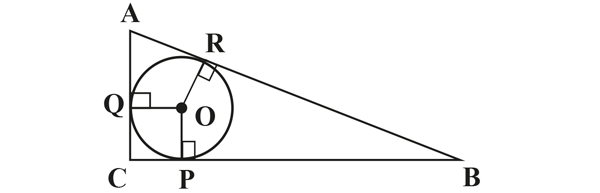
Dans le cas général, on peut tout de même relier l’aire S du triangle aux longueurs des côtés et du rayon r du cercle inscrit ; on a alors 2S = r (a + b + c).
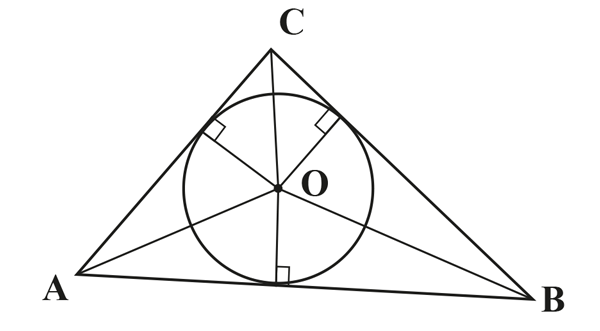
Pour le démontrer, il suffit d’additionner les aires des trois triangles OAB, OAC et OBC.
