SOLUTION
Les solutions se trouvent de manière intuitive, mais on peut bien sûr les démontrer ! Introduisons les notations suivantes.
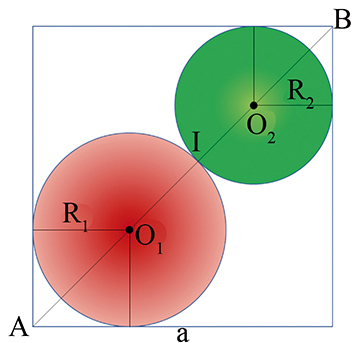
On a AO1 + O1I + IO2 + O2B = AB. En appliquant le théorème de Pythagore, on trouve AO1 = R1, AO2 =
R2 et AB =
a.
Avec O1I = R1 et O2I = R2, on déduit de l’égalité que R1 + R2 = (2 ‒ )a et donc que cette somme est constante.
Les gâteaux ayant une hauteur fixe, il suffit de s’intéresser à l’aire des deux cercles de centre O1 et O2 pour voir quand elle est minimale et maximale. On a : A = πR12 + πR22 = 2π[(3 – 2 )a + R12 ‒ (2 ‒
)a R1].
En considérant que R1 est une variable, on reconnaît une fonction quadratique (représentée par une parabole), laquelle possède un minimum.
Pour que A soit maximale, R1 doit être le plus grand possible en tenant compte de la taille de la boîte.
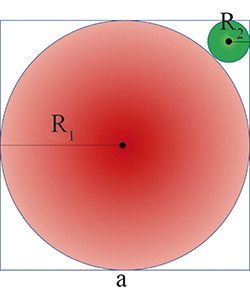
On a alors R1 = a / 2 et, par conséquent, R2 = (3 / 2 ‒√2 )a.
Pour que A soit minimale, on calcule la dérivée de A par rapport à R1 ; on trouve
2π[2R1 ‒ (2 ‒ √2 )a], qui s’annule pour R1 = (1 ‒ √2 /2)a.
Le calcul de R2 donne la même valeur. Les deux gâteaux doivent donc être identiques et on aura une surface, donc un volume, de gâteau minimal, avec un point de tangence I au centre du carré.

