Le prince Rupert du Rhin (1619-1682) est un comte palatin connu comme militaire et comme inventeur. On lui attribue un problème qu’il proposa sous la forme d’un pari : est-il possible en creusant un tunnel dans un cube sans diviser ce cube en plusieurs morceaux, de faire passer par le tunnel un cube de même taille ?
Rupert affirmait que c’était possible et il demanda au mathématicien anglais John Wallis (1616-1703) de le prouver. Wallis démontra que c’était possible et il prouva de surcroît qu’on pouvait faire traverser le premier cube par un cube légèrement plus grand.

Le prince Rupert du Rhin.

John Wallis.
La démonstration de Wallis
Le tunnel que Wallis se proposait de percer dans le premier cube avait une forme carrée et un axe confondu avec une grande diagonale du cube.
Si on projette un cube orthogonalement sur un plan selon la direction d’une de ses grandes diagonales, on obtient un hexagone régulier ABCDEF (voir la figure).
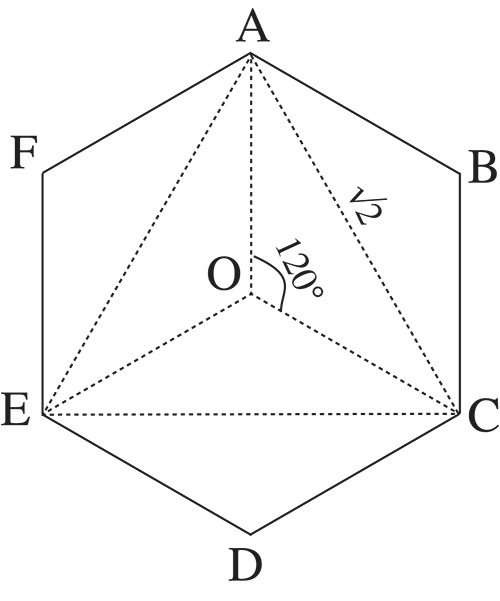
Dans cette projection, seuls les segments [AC], [CE] et [CA], qui sont dans un plan parallèle au plan sur lequel on projette le cube, voient leur longueur conservée dans la projection. Si l’arête du cube mesure 1 dm, les longueurs des côtés du triangle équilatéral ACE sont égales à (en dm).
1. Quelle est la longueur des côtés de l’hexagone régulier ABCDEF ?
Wallis construit ensuite le plus grand carré inscrit dans l’hexagone. Le tunnel perçant le cube aura une section correspondant à ce carré.
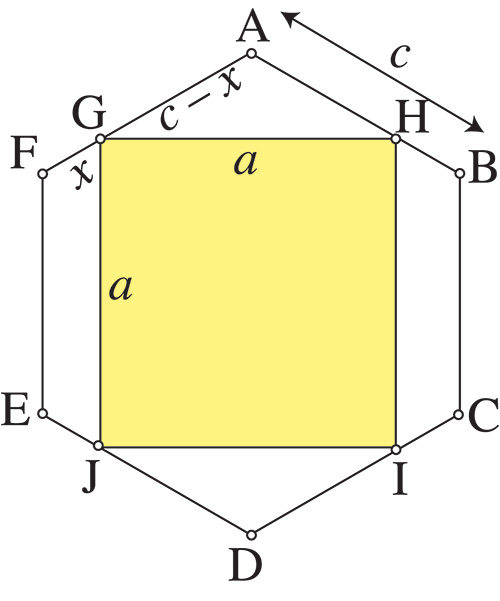
Ce carré a le même centre que l’hexagone et deux de ses côtés sont parallèles à deux côtés de l’hexagone. En effet, si ce n’était pas le cas, un déplacement ou une rotation du carré autour de son centre montrerait qu’il n’est pas maximal.
2. Calculez la longueur a du côté du carré en fonction de la longueur c du côté de l’hexagone.
La solution de Pieter Nieuwland

Pieter Nieuwland.
Près d’un siècle plus tard, le scientifique néerlandais Pieter Nieuwland (1764-1794) améliora la solution de Wallis et obtint une solution optimale avec un tunnel orienté différemment (non parallèle à une grande diagonale du cube).
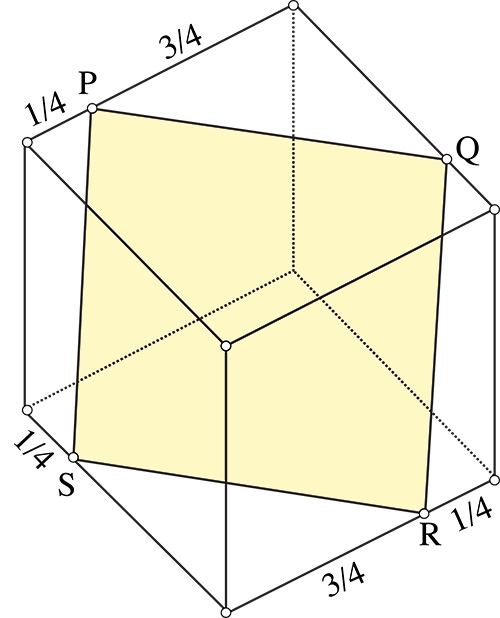
3. Vérifiez que PQRS est un carré et calculez la longueur de son côté.
Au cours des siècles suivants, ce problème fut étendu à d’autres polyèdres : peuvent-ils être traversés par un polyèdre identique au moins de même taille ?
Martin Gardner posa également la question de la généralisation à d’autres dimensions, notamment aux hypercubes.

