Lorsqu’une fraction n’est pas irréductible, on demande généralement de la simplifier en divisant numérateur et dénominateur par leur plus grand diviseur commun (PGCD). Parfois, une fausse simplification aboutit néanmoins à un résultat correct !
Lorsque l’on barre deux chiffres identiques au numérateur et au dénominateur d’une fraction, tous deux à plusieurs chiffres, et que l’on écrit la fraction obtenue avec les chiffres restants, peut-on obtenir un résultat exact ?
Éliminons déjà le cas des fractions du type , ou du type
(avec a et b deux chiffres différents), pour lesquelles la réponse est évidente. Pour deux chiffres x et y, on utilise la notation
pour signifier le nombre formé des deux chiffres x et y juxtaposés, donc le nombre dont le chiffre des unités est y et le chiffre des dizaines, x. Les fractions
et
, égales respectivement à
et à
, répondent à la question. En effet, si l’on barre les deux « 6 », les chiffres restants donnent un résultat qui est bien égal à la fraction de départ. En existe-t-il d’autres, en dehors des solutions triviales ?
Si l’on se limite à des fractions dont les deux termes (numérateur) et
(dénominateur) s’écrivent avec deux chiffres non nuls distincts en base 10, et aux fractions strictement inférieures à 1, on peut écrire :
où 0 < a < b et 0 < a < c < 10.
De cette égalité, on tire 10a (b – c) = c (b – a). On en déduit que c = 5 ou b – a = 5, l’autre facteur étant pair, et que b > c.
Si c = 5, on obtient 2a (b – 5) = b – a, d’où b (2 – 1 / a) = 9. Si b = 1 ou 3, on aboutit à une impossibilité, mais b = 6 conduit à la fraction 26 / 65, égale à 2 / 5, et b = 9 conduit à la fraction 19 / 95, égale à 1/5.
Si b – a = 5, on a 10a (b – c) = 5c, avec b > 5. On en déduit b – c = c / 2a et c = 2ab / (2a + 1) ; c est donc pair et b > c. Il existe quatre cas possibles.
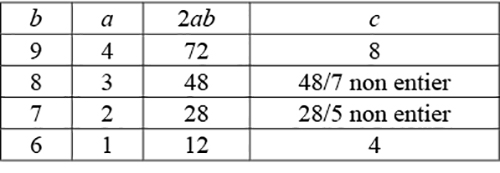
Seuls deux de ces cas conduisent à une solution : 49 / 98 = 4 / 8 = 1 / 2 et 16 / 64 = 1 / 4.
Il existe donc exactement quatre fractions non triviales inférieures à 1 dont les deux termes comportent deux chiffres distincts et qui peuvent être simplifiées en « barrant deux chiffres identiques » au numérateur et au dénominateur.
Des solutions liées par paires
Une transformation simple permet de passer d’une solution à une autre, en remplaçant a par b – c et c par b – a :
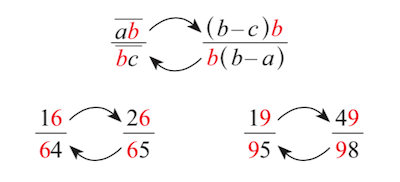
Cette transformation est involutive, c’est-à-dire que l’image de l’image d’une fraction par cette transformation est la fraction de départ.
1. Montrez que si la fraction est simplifiable en « barrant les deux b », alors la fraction
l’est aussi.
2. Montrez qu’en base 7 il n’existe aucune fraction de deux chiffres sur deux chiffres simplifiable de cette façon.

