
Question changement climatique, l’année 2024 sera-t-elle apocalyptique ? Nul ne le sait mais on espère tous que le réel décrit par Jean Dutourd dans son roman dystopique éponyme de cette nouvelle année (2024, Gallimard, 1975) ne sera pas non plus d’actualité. Par contre, l’entier 2024, lui, est apocalyptique ! En effet, l’écriture du nombre 22024, qui possède six cent dix chiffres, contient la séquence 666 à la 471e décimale. Or, un nombre n est déclaré apocalyptique si l’écriture décimale de 2n contient la séquence 666. Ce nombre 666, présent dans l’Apocalypse de Jean, dernier livre du Nouveau Testament, est appelé nombre de la Bête (voir encadré) car il symbolise la Bête sans qu’il soit possible d’expliciter clairement ce qu’elle désigne : l’empereur romain Néron, qui a persécuté les premiers chrétiens, l’Antéchrist, Satan… Tout cela est très loin des mathématiques.
2024 avec des oranges
Empilez des sphères sous forme de pyramide à base triangulaire, comme vous le feriez avec des oranges. Pour une pyramide de vingt-deux étages, il vous faudra exactement deux mille vingt-quatre sphères.
.png)
Mieux : 2024 est un nombre figuré (pour en savoir plus sur cette catégorie d’entiers, rendez-vous à la page « Les nombres figurés » , où un dossier complet leur est consacré !). En effet, c’est le huitième nombre dodécaédrique. Il est donné par la formule suivante :
C’est le nombre de points régulièrement répartis dans un dodécaèdre régulier à partir du placement de huit points sur chaque arête. Le dodécaèdre régulier fait partie des cinq solides de Platon et ses faces sont des pentagones réguliers : il possède vingt sommets, trente arêtes et douze faces. Dans la symbolique de Platon, il représentait le Tout car « s’approchant le plus de la sphère ». Aristote l’a ensuite nommé éther, a posé que l’univers était fait avec cet élément et qu’il contenait tous les autres : eau, terre, feu et air, chacun représenté par un autre solide de Platon.
Un nombre intouchable mais pratique !
Revenons aux nombres apocalyptiques, à ne pas confondre avec d’autres entiers appelés nombres de l’Apocalypse qui, eux, doivent contenir la séquence 666 dans leur écriture. Ces nombres apocalyptiques sont en nombre infini et on conjecture que tout entier n vérifiant n ≥ 29 785 est apocalyptique. Comme on peut le constater, ce n’est donc pas une propriété rare. D’ailleurs, les plus proches voisins de 2024 ayant cette propriété sont 2015, 2019, 2021 et, de l’autre côté, 2025, 2032 et 2033.
Le nombre de la Bête
666 est intervenu dans l’histoire dans de nombreux conflits entre religions. Par exemple, au XVIe siècle, catholiques et protestants l’utilisèrent, chacun de leur côté, pour s’accuser mutuellement d’incarner l’Antéchrist. Ensuite, ce furent les chrétiens qui l’utilisèrent contre les musulmans. À chaque fois, une traduction numérique de l’« ennemi » (Luther, le pape ou Mahomet) était faite et donnait pour résultat 666.

Actuellement, de nombreuses propriétés faisant intervenir ce nombre sont recherchées par les mathématiciens « amateurs », sans doute plus par jeu et par défi que par une croyance quelconque… On relève ainsi que :
• il peut s’écrire comme une somme de nombres utilisant tous les chiffres :
666 = 1 + 2 + 3 + 4 + 567 + 89 = 123 + 456 + 78 + 9 ;
• en chiffres romains, il s’écrit en utilisant chaque symbole inférieur à M une fois seulement et ce dans l’ordre décroissant : 666 = DCLXVI ;
• c’est la somme des sept premiers carrés des nombres premiers :
666 = 22 + 32 + 52 + 72 + 112 + 132 + 172 ;
• c’est une somme de cubes remarquables :
666 = 13 + 23 + 33 + 43 + 53 + 63 + 53 + 43 + 33 + 23 + 13 ;
• il est égal à la somme de ses chiffres et des cubes de ses chiffres :
666 = 6 + 6 + 6 + 63 + 63 + 63 ;
• il est lié au nombre d’or :
où
désigne le nombre d’or.
2024 a beau être apocalyptique, il est intouchable ! Cette propriété désigne un entier qui n’est pas égal à la somme de tous les diviseurs propres (appelés aussi diviseurs stricts) d’un autre entier, c’est-à-dire des diviseurs autres que cet entier. Par exemple, les diviseurs propres de 8 sont 1, 2 et 4. En conséquence, 7 n’est pas intouchable, étant la somme des diviseurs propres de 8. Le mathématicien hongrois Paul Erdős (1913‒1996) a démontré, dans les années 1970, qu’il existe une infinité de nombres intouchables et que leur densité n’est pas nulle. On conjecture que 5 est le seul entier impair intouchable. Les plus proches voisins de 2024 ayant cette propriété sont 2008, 2010, 2022 et, dans les valeurs plus grandes, 2036, 2048 et 2050.
2024 dans un triangle
Donnez-vous un disque de rayon 15. Plusieurs triangles à côtés entiers tiennent à l’intérieur. Combien exactement ? 2024, évidemment !
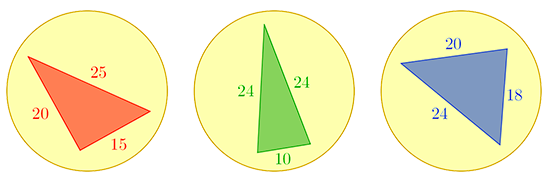
Trois des deux mille vingt-quatre triangles
à côtés entiers contenus dans un disque de rayon 15.
2024 a beau être intouchable, il est quand même pratique : tous les entiers plus petits que lui peuvent s’écrire comme une somme de certains de ses diviseurs propres, éventuellement tous. Prenons un exemple simple : les diviseurs de 16 sont 1, 2, 4, 8 et 16. Or, 1 = 1 ; 2 = 2 ; 3 = 1 + 2 ; 4 = 4 ; 5 = 1 + 4 ; 6 = 1 + 2 + 3 ; 7 = 1 + 2 + 4 ; 8 = 8 ; 9 = 1 + 8 ; 10 = 2 + 8 ; 11= 1 + 2 + 8 ; 12 = 4 + 8 ; 13 = 1 + 4 + 8 ; 14 = 2 + 4 + 8 et 15 = 1 + 2 + 4 + 8. Par conséquent, 16 est un entier pratique. On laisse les lecteurs motivés le vérifier pour 2024 ! En fait, il existe une caractérisation – certes un peu sophistiquée – des nombres pratiques à partir de leur décomposition en facteurs premiers. Il en existe une infinité mais Paul Erdős (encore lui !) et le mathématicien australien John Loxton ont démontré en 1979 que leur densité est nulle. Leurs propriétés ont été utilisées en 1202 par Leonardo Fibonacci (vers 1180 ; vers 1250) dans son livre Liber Abaci à propos des « fractions égyptiennes » mais les nombres pratiques n’ont été formalisés qu’en 1948 par le mathématicien indien A. K. Srinivasan. Les plus proches voisins pratiques de 2024 sont, parmi les valeurs inférieures, 2000, 2010 et 2016 et, parmi les valeurs supérieures, 2028, 2040 et 2046.
À partir de coordonnées entières
Quelques constructions de géométrie plane permettent d’obtenir 2024 éléments de façon assez simple.
On peut par exemple tracer toutes les droites passant par deux des seize points (en bleu sur la figure ci-dessous) à coordonnées entières situés sur les bords d’un carré de côté 4 ; on obtient alors exactement deux mille vingt-quatre polygones.
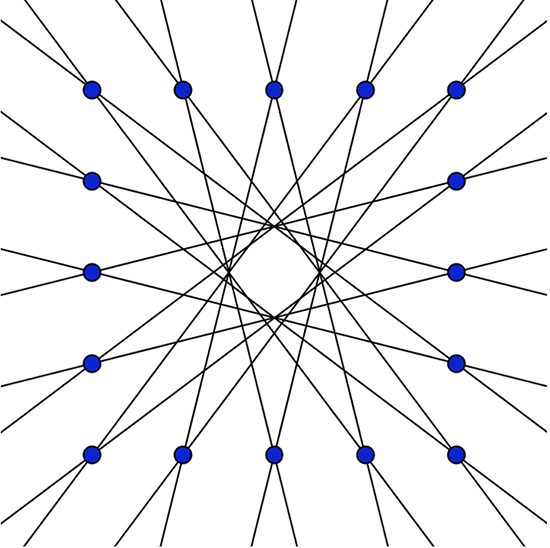
Quelques-unes des droites passant par deux des seize points
à coordonnées entières situés sur les bords d’un carré de côté 4.
Ces petits jeux de lignes passant par des points à coordonnées entières connaissent des variantes.
Prenez par exemple une grille carrée de 23 × 23 points et comptez les segments qui passent par exactement huit de ces points. Vous en trouverez exactement 2024 !
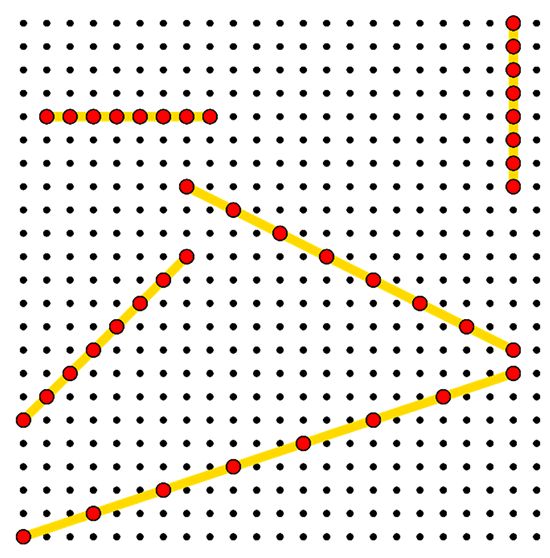
Quelques-uns des deux mille vingt-quatre segments
passant par exactement huit points du réseau 23 × 23.
2024 est un nombre sympa…
Certains peuvent penser que toutes ces propriétés rendent le nombre 2024 bien sympathique mais, de plus, il est quasi-amical ! C’est avec l’entier 2295 qu’il a cette relation : la somme des diviseurs non triviaux (différents de 1 et d’eux-mêmes) de chacun de ces entiers est égale à l’autre. En effet, les diviseurs non triviaux de 2024 sont 2, 4, 8, 11, 22, 23 44, 46, 88, 92, 184, 253, 506 et 1012 : leur somme vaut 2295. De même, les diviseurs non triviaux de 2295 sont 3, 5, 9, 15, 17, 27, 45, 51, 85, 135, 153, 255, 459 et 765, dont la somme vaut 2024.
On notera la ressemblance avec la définition des nombres amicaux où la somme qui intervient est celle des diviseurs propres. Et, comme pour les nombres amicaux, cette propriété est très rare : il n’y a que quatre-vingt-six entiers inférieurs à 108 la possédant. Elle est même plus rare que la propriété d’être amical puisqu’il y a deux cent trente-six nombres amicaux inférieurs à 108.
Les plus proches voisins de 2024 ayant cette propriété sont, d’un côté, 1575 et 1648 et, de l’autre, 5775 et 6128. Comme pour les nombres amicaux, on ignore s’il en existe une infinité, mais contrairement à eux, on ne sait pas s’il existe un couple de nombres quasi-amicaux de même parité. Pour les nombres amicaux, c’est l’inverse : c’est l’existence d’un couple de parité différente qui est inconnu.
Alors si on vous dit que 2024 sera une année banale, ne le croyez pas !
L’arithmétique de 2024
En arithmétique, 2024 est la somme des carrés des entiers pairs de 2 à 22 et la somme des cubes de 2 à 9. C’est également le nombre de produits différents que l’on peut obtenir en multipliant trois entiers (éventuellement égaux) compris entre 1 et 31. Cela ne représente qu’un peu moins de 6,8 % des 29 791 entiers compris entre 1 et 313.
Maintenant, imaginons que vous souhaitiez ranger onze délicieux chocolats aux parfums différents dans deux boîtes distinctes. Vous avez deux choix pour chaque friandise, ce qui donne un total de 211 = 2 048 rangements différents.
Si les boîtes ne peuvent contenir que neuf chocolats au maximum, alors le nombre de rangements différents descend à 2 024.
Voici enfin une autre particularité plus corsée : 2024 est le nombre de solutions entières de l’équation x 2 + y 2 + z 2 ≡ 1 mod 46.



