
L’un des plus célèbres problèmes de coloriage porte sur le « nombre chromatique du plan ». Qu’est-ce donc ? Le but est d’attribuer une couleur à chaque point du plan de façon que deux points distants d’une unité soient toujours de couleurs différentes. Évidemment, le but du jeu est d’utiliser le moins de couleurs possible, et c’est ce nombre minimal que l’on appelle nombre chromatique du plan, noté χ (ℝ2).
L’examen d’un simple triangle équilatéral permet de se convaincre que χ (ℝ2) ≥ 3. En 1961, le mathématicien canadien Leo Moser (1921‒1970) a proposé un graphe, parfois baptisé broche ou fuseau de Moser, qui permet de constater que χ (ℝ2) ≥ 4. Il a été rapidement établi que χ (ℝ2) ≤ 7. mais il aura fallu ensuite attendre 2018 pour que l’encadrement soit amélioré ; la question reste aujourd’hui ouverte (voir encadré).
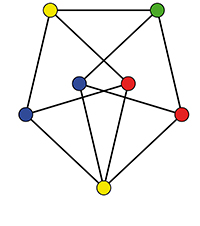
Le fuseau de Moser.
Avec une seule couleur !
Si vous n’avez pas de boîte de crayons de couleur sous la main et seulement un stylo noir, rien ne vous empêche de vous confronter à de belles questions de coloriage pour autant. Dans les années 1960, Leo Moser avait en effet proposé un autre problème moins connu mais tout aussi amusant : quelle proportion maximale du plan peut-on colorer de manière que deux points ... Lire la suite
