
La nouvelle année est souvent l’occasion d’amusements divers autour des nombres. Voici, par exemple, quelques égalités reçues de Gérard Crézé, de Saint-Michel en l’Herm :
(1 + 2) × 3 + 4 × 56 × (−7 + 8) × 9 = 2025 ;
(1 × 2 + 34) × 56 + (−7 + 8) × 9 = 2025 ;
− (1 + 2 × 3) + (34 − 5) × 67 + 89 = 2025.
Le jeu connaît un certain engouement depuis 2011, année lors de laquelle le réalisateur Takeshi Kitano a proposé, à l’occasion d’une exposition d’art contemporain, de trouver une expression du millésime de l’année constituée des premiers entiers écrits dans l’ordre, séparés par des opérateurs mathématiques usuels (+ , − , × , / , racine carrée, factorielle et exposants).
Pour l’année 2025, on a par exemple : − (1 + 2) + (3!)4 + 5 + 6! + 7 = 2025.
Vous en trouverez certainement beaucoup d’autres ! Parviendrez-vous à utiliser encore moins d’entiers que les sept premiers ?
Encore des carrés !
2025 est un carré qui entretient des liens étroits avec d’autres carrés. C’est, par exemple, un carré dont la somme des chiffres est aussi un carré. La dernière fois que cela était arrivé, c’était en 1681 et la prochaine fois, ce sera en 2304.
Remplacez chaque chiffre de 2025 par son successeur : vous trouverez encore un carré (ici 3136, le carré de 56). La prochaine fois, ce sera en 13 225 ; en effet, 13 225 = 1152 et 24 336 = 1562.
2025 est aussi le plus grand carré qui s’écrit avec 11 chiffres en base 2 (11111101001) et un des 33 carrés qui peuvent apparaître sur l’écran d’un radio-réveil (à 20 : 25) !

Des liens forts avec 45
Bien des particularités du nombre 2025 méritent d’être signalées. Plusieurs d’entre elles sont liées à sa racine carrée, qui vaut 45, un nombre dont l’écriture en base 2 est palindromique (c’est 101101). Comme tous les carrés de nombres impairs, 2025 est un nombre octogonal centré. Autrement dit, il peut être représenté par un ensemble de points qui forment des octogones réguliers concentriques de côtés 0, 1, 2, 3, etc.
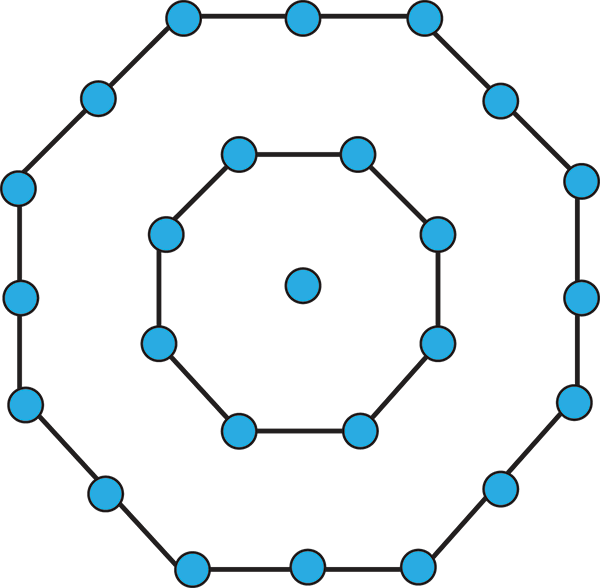
25 est un nombre octogonal centré.
Les trois octogones sont constitués de 1, 8 et 16 points.
Pour comprendre pourquoi les nombres octogonaux centrés coïncident exactement avec les carrés impairs, on peut suivre la démonstration sans mots, mais non moins éloquente, donnée ci-dessous sur deux cas particuliers.
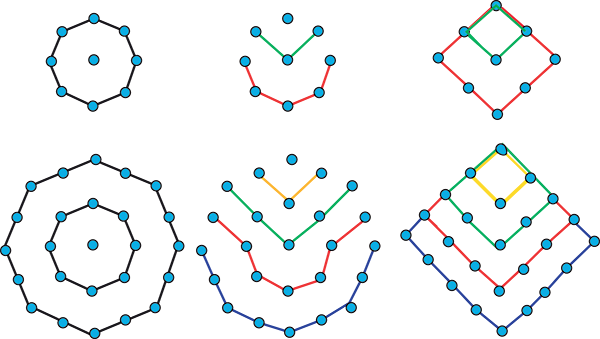
Transformation de nombres octogonaux centrés en nombres carrés.
Le nombre 2025 peut donc être représenté par 23 octogones concentriques, le plus grand étant constitué de 176 points.
Les liens surprenants entre 2025 et sa racine carrée ne s’arrêtent pas là ! Sans doute connaissez-vous les nombres premiers jumeaux, ces nombres premiers séparés seulement de deux unités comme 5 et 7, 11 et 13 ou encore 29 et 31. Entre 2025 et son double, plusieurs nombres premiers p ont un frère jumeau supérieur (de la forme p + 2) et il y en a exactement 45.
Autre amusette, essayez de donner une partition de 45 en au moins trois entiers distincts. Par exemple, 45 = 2 + 3 + 10 + 30 ou 45 = 14 + 15 + 16 sont de telles décompositions, mais 45 = 20 + 25 ou 45 = 10 + 10 + 25 ne le sont pas. Vous devriez en trouver un bon nombre ; il y en a exactement 2025.
Des sommes à n’en plus dormir !
Puisque nous évoquions les nombres figurés, sans doute avez-vous déjà entendu parler des nombres triangulaires. Ce sont les nombres qui s’obtiennent comme la somme des premiers entiers consécutifs : Tn = 1 + 2 + 3 + … + n = n (n + 1)/2.
Le nombre 2025 étant un carré, il est la somme de deux nombres triangulaires consécutifs : 2025 = T44 + T45.
De façon générale, vous pourrez vérifier par un simple calcul algébrique que
n2 = Tn–1 + Tn.
Mais 2025 est également le carré d’un nombre triangulaire puisque :
45 = T9 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
et, à ce titre, il est égal à la somme des premiers cubes d’entiers naturels :
2025 = T92 = 13 + 23 + 33 + 43 + 53 + … + 93.
Plusieurs démonstrations élégantes de cette relation, Tn2 = 13 + 23 + … + n3 (appelée théorème de Nicomaque) ont été données depuis l’Antiquité à l’aide de jolis découpages.
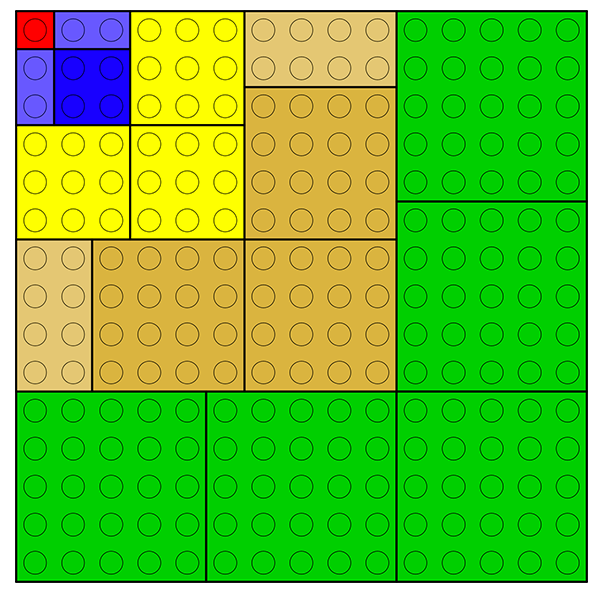
La surface de ces plaques d’un célèbre jeu de construction
est égale au carré de la somme des entiers de 1 à 5.
En les empilant par couleur, on peut aussi construire les cubes de côtés 1 à 5.
On démontre de même que 2025 est la somme des cubes de 1 à 9.
Le nombre 2025 n’est pas sans rappeler également le théorème des deux carrés de Fermat, dit aussi théorème de Noël car il a été longuement commenté par le magistrat de Toulouse dans une lettre au Père Mersenne datée de Noël 1640. Ce théorème stipule qu’un entier est la somme de deux carrés si, et seulement si, chacun de ses facteurs premiers de la forme 4k + 3 intervient avec un exposant pair.
Ici, nous avons 2025 = 34 × 52 donc les conditions s’appliquent. Carl Gustav Jakob Jacobi (1804-1851) apportera même quelques précisions permettant de connaître le nombre de décompositions en somme de deux carrés ; pour 2025, il n’y en a qu’une seule :
2025 = 272 + 362. Si on s’autorise à additionner un peu plus de carrés, le nombre 2025 offre une nouvelle propriété : c’est le plus petit carré qui puisse s’écrire comme une somme de 17 carrés distincts.
Saurez-vous trouver une telle décomposition ?
À titre indicatif, on peut utiliser le carré de 23.
2025 et ses diviseurs
On l’a vu, 2025 est divisible par 45 dont il est le carré. En tout, il compte 15 diviseurs et c’est d’ailleurs le plus petit nombre impair en ayant autant (On peut aussi dire que c'est le plus petit impair ayant 15 diviseurs). C’est aussi un nombre refactorisable (ou nombre tau), c’est-à-dire qu’il est divisible par son nombre de diviseurs puisque 2025 = 15 × 135. Il existe une infinité de nombres refactorisables et bien des conjectures pourtant simples à exprimer restent encore à démontrer à leur sujet. Notre millésime est aussi le plus petit multiple de 15 ayant 15 diviseurs. Ce dernier résultat est peut-être plus étonnant qu’il n’y paraît ; à titre comparatif, le plus petit multiple de 13 ayant 13 diviseurs est 23 298 085 122 481.
Enfin (ou « en faim » ?), 2025 est aussi un nombre fourchette (ou gapful) c’est-à-dire qu’il est divisible par le nombre à deux chiffres formé en concaténant son premier et son dernier chiffre : 2025 = 25 × 81. Voyez-vous en quelle année cela arrivera à nouveau ?
Dans l’œuvre de Kaprekar
Le nombre 2025 apparaît également dans l’œuvre du mathématicien indien Dattatreya Ramachandra Kaprekar (1905-1986) dont les travaux en arithmétique ont été diffusés auprès du grand public par Martin Gardner. Il s’est, en effet, intéressé aux nombres qu’il a qualifiés d’harshad (« qui donne de la joie », en sanscrit) et qui sont divisibles par la somme de leurs chiffres. C’est bien le cas de 2025, qui est divisible par 2 + 0 + 2 + 5 = 9.
Comme on l’a souvent vu ici, le nombre 2025 tire une partie de son intérêt du fait qu’il est le carré de 45. Il se trouve que 45 est un nombre de Kaprekar. Cela signifie qu’on peut scinder son carré en deux nombres dont la somme vaut justement 45.
En effet, 452 = 2025 et 20 + 25 = 45. Les prochaines années où ce phénomène pourra être observé sont 3025, 9801 et 88209 pour laquelle on a bien (88 + 209)2 = 88 209.

Dattatreya Ramachandra Kaprekar.
Des questions de géométrie discrète
Quittons maintenant le monde de l’arithmétique pour aborder celui de la géométrie discrète ou de la combinatoire. Pour commencer, partons d’un carré et découpons chaque côté en n segments de même longueur. On obtient alors 4n points disposés en carré. Relions chaque point à celui situé n + 1 points plus loin. Comme un schéma vaut souvent mieux qu’un long discours, voyez le joli dessin obtenu pour n = 3. On y compte alors 37 régions.
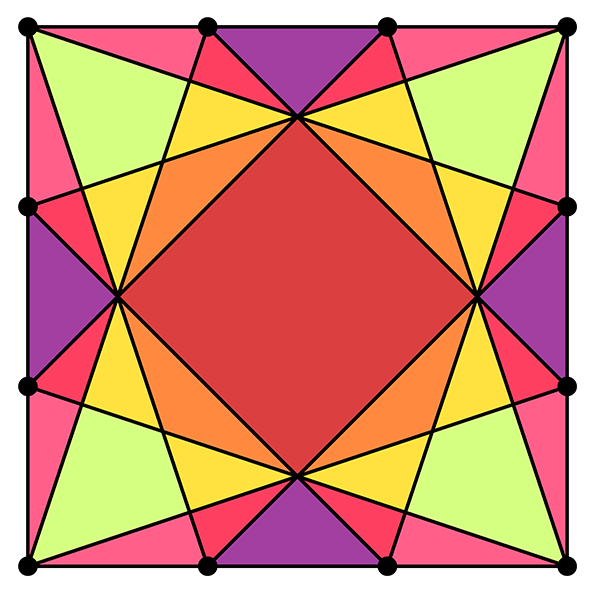
Et avec n = 22 ? On obtient 2025 régions, bien sûr ! Attention, l’étude du cas général ne s’avère pas si simple.
Vous êtes-vous déjà demandé de quelle façon on pouvait représenter un disque sur une image pixelisée ? Voici une méthode possible. Plaçons-nous dans une grille constituée de petits carrés. Si on trace un cercle de rayon 5 dont le centre est le centre d’un des petits carrés, ce cercle contient 61 petits carrés.

Pour un cercle de rayon 26, on trouvera 2025 petits carrés entiers ! Un « petit » coloriage devrait vous permettre de vous en convaincre !
Le nombre 2025 se cache aussi dans une belle énigme de théorie des graphes. Placez quatre points dans le plan et reliez-les tous les uns aux autres. Vous obtenez le graphe complet d’ordre 4, noté K4. Combien de croisements avez-vous réalisés ? En vous y prenant bien, peut-être aucun, par exemple en plaçant un des points à l’intérieur du triangle formé par les trois autres.
Essayez-donc avec le graphe K5. Il est possible de le dessiner avec un seul croisement mais on ne peut pas faire mieux. Pour K6, on sait que le minimum est de 3 croisements et que, pour K7, il est de 9 croisements. Démontrer ces premiers résultats n’est déjà pas si évident.
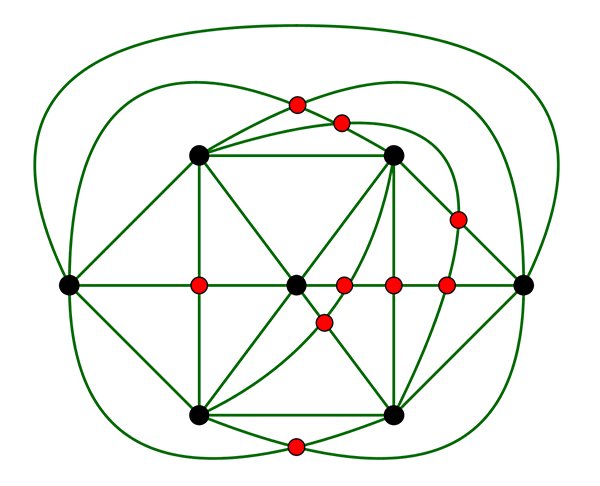
Une représentation de K7 avec 9 croisements (en rouge).
On peut démontrer qu’il n’est pas possible de faire mieux.
Toutes les valeurs sont connues jusqu’à K14 mais ensuite, rien n’est certain. Pour K21, on conjecture que le minimum est de 2025 croisements. Qui arrivera à le démontrer ? Même si nous ne le saurons peut-être pas avant la fin de l’année, espérons que celle-ci soit des plus heureuses pour nos lectrices et nos lecteurs !
Après les carrés, les rectangles…
En traçant 7 droites dans le plan, on ne peut pas obtenir plus de 18 rectangles.
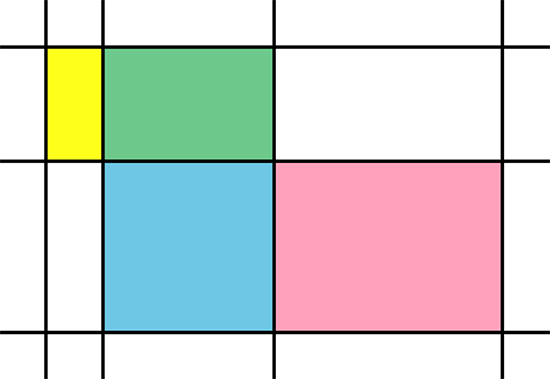
Arrivez-vous à compter les 18 rectangles dans cette figure ?
Avec 20 droites on ne peut pas obtenir plus de 2025 rectangles. Voyez-vous comment disposer les droites pour y parvenir ?
Il faut en mettre 10 à l’horizontale et 10 à la verticale.
Décrire un rectangle revient alors à choisir 2 des 10 droites horizontales et 2 des 10 droites verticales.
Or il y a façons de choisir 2 droites parmi 10
ce qui donne bien en tout 45 × 45 = 2025 rectangles.
On conjecture que le nombre maximum de rectangles qu’on puisse obtenir avec n droites est égal au nombre minimum de croisements pour le graphe Kn+1 mais cela reste à démontrer…
