
Pour un nombre n de côtés, on détermine ainsi le plus grand petit n-gone.
Dans le cas d’un quadrilatère, l’aire est égale à e × f × sin(θ)/2, où e et f sont les longueurs des diagonales et θ leur angle (voir en page 18).
Son maximum est atteint pour e = f = sin(θ) = 1.
Ceci correspond à une infinité de quadrilatère, dont le carré.
Pour n impair, Karl Reinhardt a montré en 1922 que la solution unique était le polygone régulier.
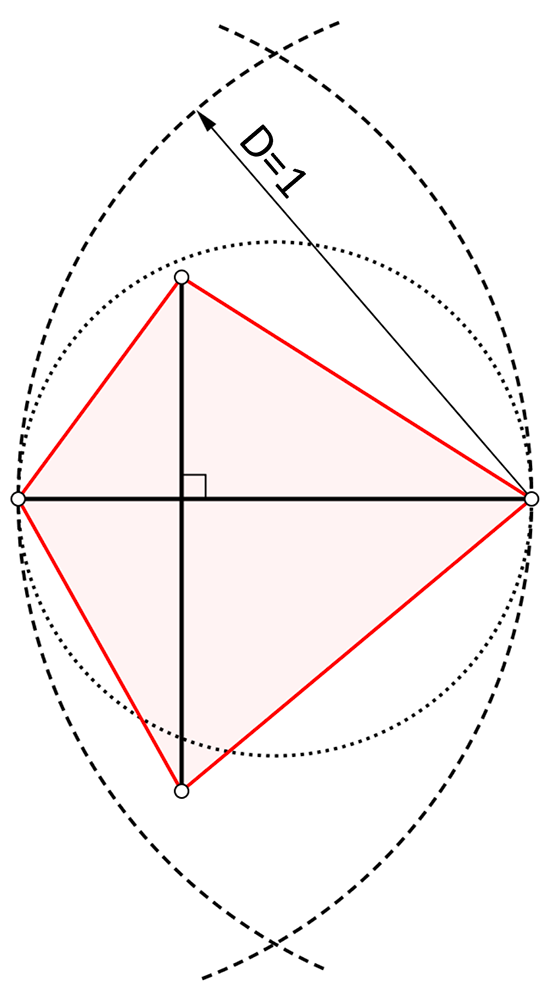
Un quadrilatère de diamètre 1 et d’aire maximale.
Pour n = 6, la solution unique n’est pas régulière. Ronald Graham détermina en 1975 qu’elle était constituée d’un pentagone irrégulier équidiagonal, avec un triangle isocèle sur l’un de ses côtés.
Son aire, d’environ 0,67498, est solution d’une équation du dixième degré ! Il conjectura qu’il en était de même pour tout nombre n de côtés pair, à savoir un triangle isocèle accolé à un (n – 1) - gone équidiagonal, ce qui fut prouvé en 2007 par le hongrois Tamás Szabo.
