Un petit joyau de Gauss

Pour un pentagone A₁A₂A₃A₄A₅, notons a_i l’aire du triangle « de coin » de sommets A_i et ses deux voisins. 

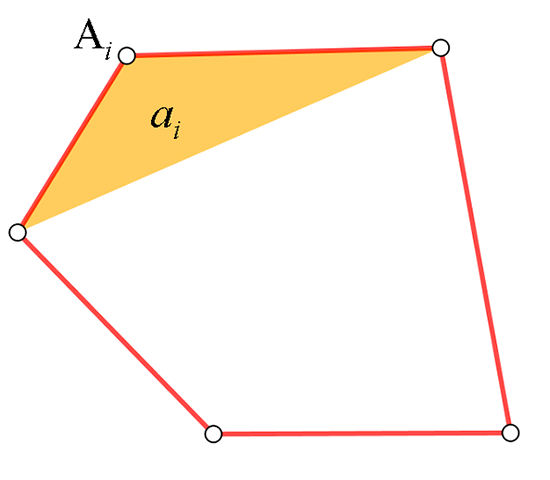
Un triangle de coin de Gauss.

Gauss a démontré que l’aire du pentagone est la plus grande racine du polynôme

x² – sx + p où s = a₁ + a₂ + a₃ + a₄ + a₅ et p = a₁a₂ + a₂a₃ + a₃a₄ + a₄a₅ + a₅a₁.

Dans le cas du pentagone régulier, en notant a l’aire du triangle de coin,on a s = 5a,

p = 5a², et donc l’aire du pentagone régulier vaut   φ étant le nombre d’or.

Cette relation est en fait équivalente à celle attribuée à Gaspard Monge :

a₂₃a₄₅ + a₂₅a₃₄ = a₂₄a₃₅ où a_ij désigne l’aire du triangle A₁A_iA_j.

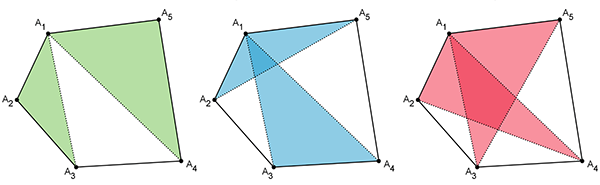
Triangles en jeu dans la formule de Monge.

L’équivalence entre les deux formules se fait en remarquant que si les trois sommets A₁, A_i, A_j sont à la suite, alors a_ij est un des a_i, et que sinon nous avons a_ij = A – a_k – a_l, où A est l’aire du pentagone et les valeurs distinctes (i, j, k, l ) sont prises dans l’ensemble (2, 3, 4, 5). Par exemple, a₃₄ = A – a₂ – a₅.

La relation de Monge se démontre, quant à elle, en recourant aux seules formules élémentaires de calcul d’aire de triangle.