
Il démontre en 1725 que si un polygone A1 A2… An d’un nombre pair de côtés est circonscrit à un cercle, on a A1A2 + A3 A4 + A5 A6 + … = A2 A3 + A4 A5 +…, et étend ce théorème au cas d’un polygone avec un nombre impair de côtés.
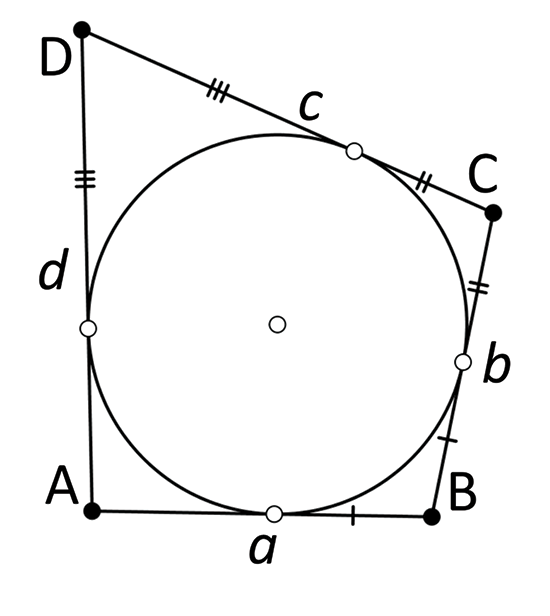
Pour un quadrilatère, on montre facilement, au vu de l’égalité des tangentes issues d’un point, que la somme des côtés opposés est égale au demi-périmètre du quadrilatère :
a + c = b + d.
Laconiques coniques
On rappelle qu’une branche d’hyperbole est l’ensemble des points M tels que la différence des distances aux deux foyers A et B est constante et que sa tangente est bissectrice de l’angle
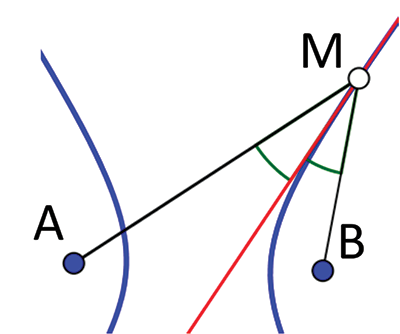
Par cette propriété classique, Gaston Darboux (1842-1917) donne une démonstration très simple de la réciproque de Steiner (voir ci-dessous). Supposons par exemple que AB + CD = BC + AD, soit BA – DA = BC – DC. Les points A et C sont donc sur l’hyperbole de foyers B et D et leurs tangentes se rencontrent en un point O à égale distance des côtés du quadrilatère, donc centre du cercle inscrit à ce quadrilatère.
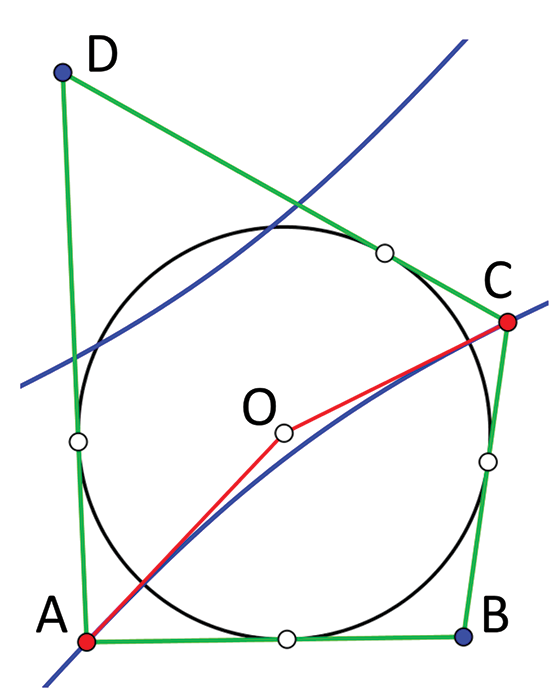
La réciproque de Steiner
Un cercle ... Lire la suite gratuitement
