Prenez une feuille de papier et réalisez votre pliage favori : une grue, un avion ou un parasaurolophus. L’important ici est de vous livrer à un pliage à plat, c’est-à-dire une réalisation que vous pourriez glisser dans les pages d’un livre sans l’abîmer. Si vous dépliez cette création, vous obtenez une feuille marquée de plis montagne, de plis vallée, et de quelques plis qui ne sont finalement pas utiles à l’objet final. La réalisation se résume ainsi par un schéma où l’on fait figurer par des segments rouges les plis montagnes et par des segments bleus les plis vallées. C’est ce que l’on appelle le canevas de plis ou la carte de plis (crease pattern en anglais).
Des théorèmes dans les canevas
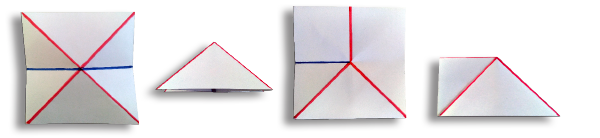
Les canevas de plis recèlent quelques trésors. On peut déjà regarder des cas très simples. Il est bien difficile de visualiser le rendu final à partir d’un canevas. Cependant, ces cartes suffisent aux origamistes les plus avertis pour communiquer entre eux leurs réalisations.
Quelques canevas très simples.
Que pouvez-vous remarquer en observant ces canevas ? Qu’en est-il du nombre de plis partant de chaque sommet ? De leur type (montagne ou vallée) ? Et des angles qu’ils forment ? Toutes ces questions trouvent ... Lire la suite