
Le solfège du plieur
On la retrouve au Japon, à partir du VIIe siècle : l’origami y est utilisé pour son aspect symbolique, lors de cérémonies, comme porte-bonheur ou dans le cadre d’échanges de cadeaux. Des exemples de pratiques de papiers pliés ont aussi été signalés en Allemagne, en Espagne ou en Italie mais pas avec la même dimension. Il est difficile de retracer l’histoire de cet art car le savoir se transmettait oralement, par la démonstration.
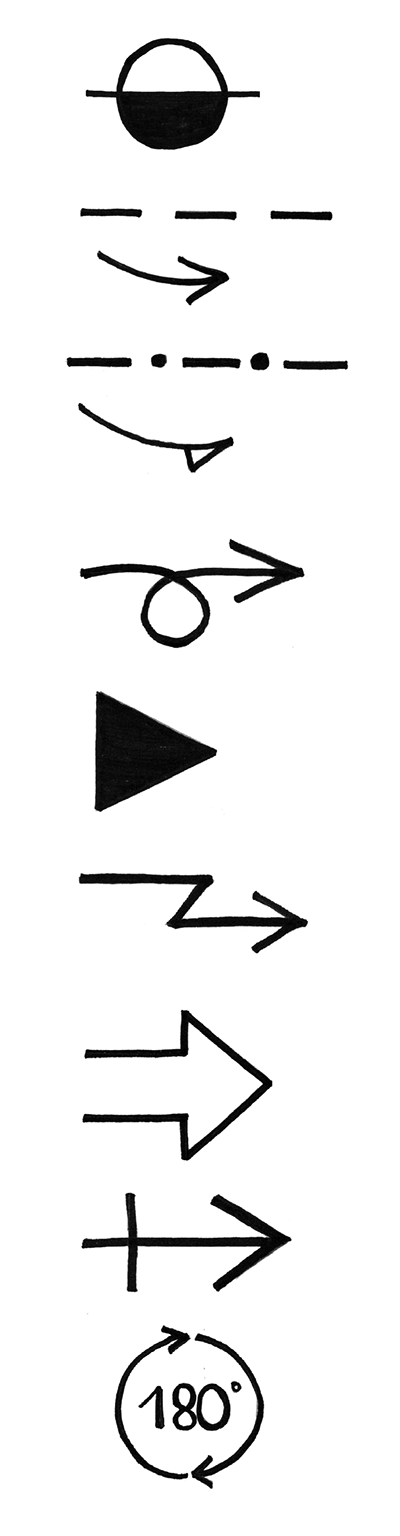
L’origami a connu un véritable renouveau lorsque des livres présentant des instructions ont été publiés, notamment grâce à de grands maîtres comme Akira Yoshizawa (1911 — 2005). Depuis, un « solfège du plieur » a été mis en place afin de codifier toutes les étapes permettant de réaliser les pliages. Des pointillés différents désignent les plis en montagne ou en vallée, une petite dizaine de flèches permettent de distinguer les actions de plier, de déplier, de plier l’avant ou l’arrière, le fait d’ouvrir le modèle, de le retourner, de répéter une opération, d’effectuer une rotation d’un angle donné… L’apprentissage de ce solfège associé à celui de quelques figures de base permet de se lancer sereinement sur des modèles de plus en plus élaborés.
Jacques Justin, l’art et la théorie du pliage
Le Mouvement français des plieurs de papier (MFPP) doit beaucoup à l’un de ses membres fondateurs, le mathématicien Jacques Justin (1926 — 2020). Ce dernier a contribué à l’élaboration des sept axiomes de l’origami, nommés axiomes de Justin–Huzita–Hatori (voir ci-dessous). Humaki Huzita (1924 — 2005) était un mathématicien et artiste italo-japonais, Koshiro Hatori (né en 1961) est un auteur japonais d’ouvrages sur l’origami. À eux trois, ils ont codifié tous les plis possibles sur une feuille de papier en fonction de ses droites et de ses points. Les six premiers axiomes ont été découverts par Justin en 1989 puis redécouverts par Huzita en 1991, et le septième énoncé en 2002 par Hatori.
Les innombrables articles de Justin dans la revue Le Pli éditée par le MFPP, dans PLOT, de la Régionale APMEP d’Orléans-Tours, ou encore L’Ouvert, de l’IREM de Strasbourg, font encore référence aujourd’hui.
Les sept axiomes de l’origami
• Étant donnés deux points p 1 et p 2 distincts, il existe un seul pli qui passe par p 1 et p 2.
• Étant donnés deux points p 1 et p 2 distincts, il existe un seul pli qui amène p 1 sur p 2.
• Étant données deux droites d 1 et d 2 distinctes, il existe un seul pli qui amène d 1 sur
d 2.
• Étant donnés un point p et une droite d, il existe un unique pli perpendiculaire à d qui passe par p.
• Étant donnés deux points distincts p 1 et p 2 et une droite d, il existe un seul pli qui place p 1 sur d et qui passe par p 2.
• Étant donnés deux points p 1 et p 2 distincts et deux droites d 1, d 2 distinctes, il existe un seul pli (le pli de Beloch) qui place p 1 sur d 1 et p 2 sur d 2.
• Enfin, étant donnés un point p et deux droites d 1 et d 2 distinctes, il existe un pli unique qui place p sur d 1 et qui est perpendiculaire à d 2.

Coquille Saint-Jacques, par Éric Joisel.
Une nouvelle géométrie
La géométrie de l’origami est une discipline très récente. Comme les autres géométries, elle repose sur un certain nombre d’axiomes (sept ici, voir ci-contre), qui permettent de déduire propositions et théorèmes. L’article Origami et Pliages pour construire (dans Bibliothèque Tangente 78, 2022) les détaille tous et donne quelques résultats auxquels ils permettent d’accéder. En particulier, il est possible à l’aide des axiomes de construire des longueurs impossibles à obtenir à la règle et au compas. On résout ainsi, en géométrie origamique, les problèmes de duplication du cube et de trisection de l’angle (voir article « Des constructions à foison »).
