
Lorsque l’on parle de l’éloignement entre deux objets « relativement proches », on fait référence à la distance euclidienne. Pourtant, quand on évoque la distance entre deux villes, ce n’est aucunement d’elle dont il s’agit. Compte tenu de la rotondité de la Terre, la distance à vol d’oiseau désigne la longueur de la plus petite des deux parties du grand cercle terrestre joignant les deux lieux (voir En Bref « Distances sur une sphère »). Quant à celle donnée par le GPS de votre voiture, elle tient compte du tracé des routes (voir En Bref « Le GPS et le plus court chemin »). Mais aussi, quel intérêt a-t-on à développer la notion de distance en mathématiques ?
Une définition axiomatique
Dire que la distance est un réel positif associé à deux points semble un préalable acceptable par tous. Ainsi nomme-t-on distance toute application δ qui, à tout couple d’éléments (a, b) d’un ensemble E, associe un réel positif ou nul noté δ (a, b)… mais cela ne suffit pas.
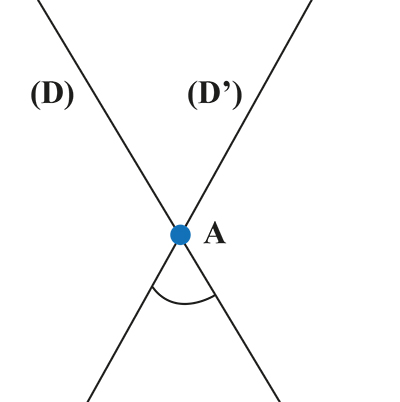
Une distance possible sur l’ensemble des droites passant par un point A donné.
Dans une axiomatique, tout ce qui ne découle pas des autres axiomes doit être ... Lire la suite
