
Premiers pas
La distance d’un point M à une courbe (C) est la plus petite des distances de M à un point m décrivant (C). Dire que M est équidistant de deux courbes (C1) et (C2) signifie alors que Mm1 = Mm2, m1 et m2 réalisant chacun le minimum de distance de M à un point m de la courbe (C1) ou (C2).
La distance d’un point M à un cercle (C) de centre F et de rayon r se matérialise ainsi par la longueur MP, où P est le point de (C) « le plus proche » de M. Il est aligné avec M et F.
Point et cercle
Lorsque A appartient à (C), la courbe d’équidistance du point A et du cercle (C) de centre F est la demi-droite [FA). Sinon, deux cas se présentent.
Dans le premier cas, A est extérieur à (C) : écrire que MP = MA revient à dire MF – r = MA, soit MF – MA = r. C’est dire, par définition, que M décrit l’hyperbole de foyers A et F et de distance entre les sommets égale à r. Il n’y a aucun point de la courbe d’équidistance intérieur au cercle (C).
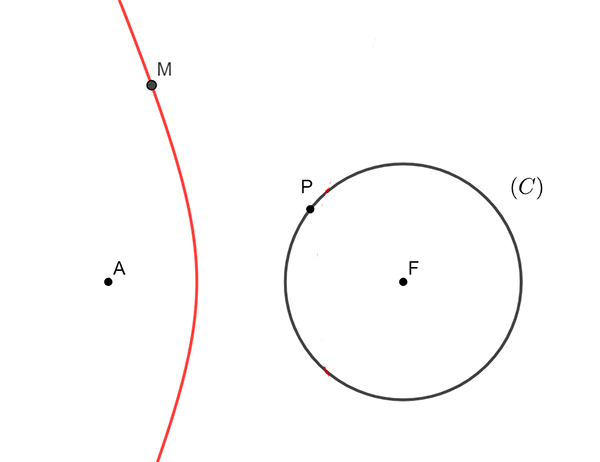
Dans le second cas, ... Lire la suite
