
La méthode des trapèzes

Considérons une fonction continue f positive, définie sur un intervalle [a, b]. On peut interpréter l'intégrale comme l'aire située entre le graphe de f et l'axe des abscisses (entre a et b). Traçons alors le trapèze limité par la courbe, l'axe des abscisses et le segment [AB].
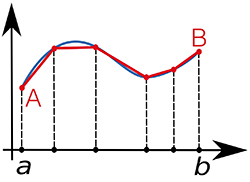
Si la fonction f possède une croissance (ou une décroissance) « assez régulière », c'est-à-dire que sa dérivée seconde varie « assez peu », on voit que l'aire du trapèze est « proche » de l'intégrale étudiée. On peut approximer la seconde par la première, soit par (b – a)(f(a) + f (b)) / 2. Ainsi, si a = 1, b = 2 et f (x) = 1 / x, on obtient
que l'on approxime par (1 + 1 / 2) /2 = 0,75.
L'erreur est d'autant plus importante que l'intervalle est grand et que la fonction y admet de fortes variations. Aussi a-t-on l'idée de partager en n parties égales l'intervalle initial, d'appliquer la méthode ci-dessus à chacun de ces n intervalles et de faire la somme. On obtient ainsi une approximation de
en posant h = (b – a) / n, par :
En reprenant notre exemple avec n = 4, on obtient I4 = 0,6845, soit une erreur inférieure à un centième !
La rigueur veut bien sûr que l'on majore l'erreur de manière théorique. Si la fonction f est deux fois dérivable et si cette dérivée seconde est bornée, majorée en valeur absolue par un nombre M, alors l'erreur est elle-même majorée par M (b – a)3 / 8n2. En particulier, si n tend vers l'infini, l'erreur tend vers 0, ce qui permet de trouver le résultat de avec une erreur aussi petite que l'on veut.
L'intégrale double
Si g est une fonction à valeurs réelles, définie sur une partie D du plan, on peut la visualiser comme une surface formée des points de coordonnées (x, y, z) où z = g (x, y) et où (x, y) appartient au domaine de définition D. Par analogie à l'intégrale sur un segment, on souhaite, si la fonction est positive, que l'intégrale sur D corresponde au volume situé entre le plan {z = 0} et la surface dans les limites du domaine D. La construction rigoureuse d'une telle intégrale est possible, avec quelques restrictions, mais… longue et délicate (voir le Calcul intégral, Bibliothèque Tangente 50, 2014).
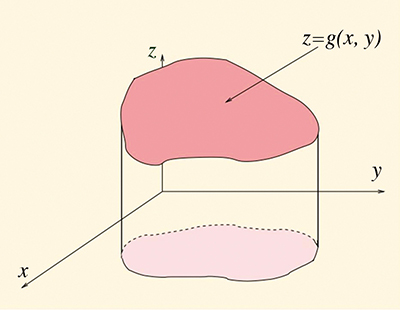
Prenons d'abord le cas où g est continue et D = [a, b] × [c, d] est un rectangle. La fonction ayant deux variables (x et y), on peut intégrer d'abord par rapport à x entre a et b, puis par rapport à y entre c et d, ou l'inverse. Miracle, le théorème de Fubini nous assure que les deux résultats coïncident et que l'on peut effectivement intervertir les deux ordres de calcul !
