Le modèle de graphe aléatoire d’Erdős et Rényi est si célèbre en mathématiques qu’il est devenu un nom commun : on parle couramment d’un « Erdős-Rényi » en probabilités comme on parlerait d’un Brillat-Savarin en gastronomie ou d’un stradivarius en musique.
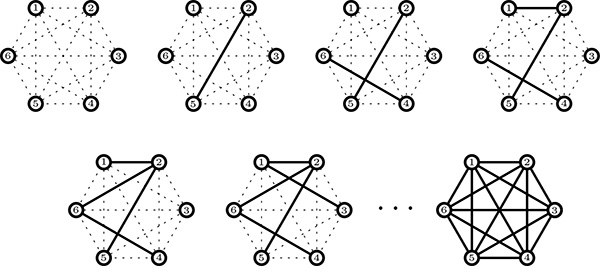
De nos jours, on regroupe souvent plusieurs modèles voisins sous l’appellation « Erdős-Rényi » et le plus naturel d’un point de vue probabiliste est certainement le suivant. On se fixe un entier naturel n ≥ 1 et l’on considère l’ensemble de sommets { ①, ②, …, ⓝ} où chaque paire de sommets distincts forme une arête.
Il y a donc 
arêtes possibles ( est bien sûr le coefficient binomial habituel, c’est-à-dire le nombre de manières de choisir 2 objets parmi n) et ces arêtes sont ajoutées l’une après l’autre uniformément au hasard. Ce procédé génère une suite croissante de graphes aléatoires (les arêtes étant ajoutées aléatoirement) notés
 \subset G(n,1) \subset ... \subset G(n,m) \subset ... \subset G\left( n, {n \choose 2}\right) )
où G(n, m) est le graphe obtenu après l’ajout de m arêtes.
En particulier, G(n,0) est composé de n sommets isolés alors que )
est le graphe complet, voir la figure ci-dessous.
Une instance de la suite aléatoire (G(6, m) : 0 ≤ ... Lire la suite
