
Lorsqu’on se trouve à l’intérieur d’un triangle, il est clair qu’on est plus proche des côtés que des sommets, mais de combien ? En 1935, Erdős propose la conjecture suivante : la moyenne des distances aux côtés est inférieure ou égale à la moitié de celle des distances aux sommets, et il n’y a égalité que lorsque le triangle est équilatéral et que l’on se trouve en son centre.
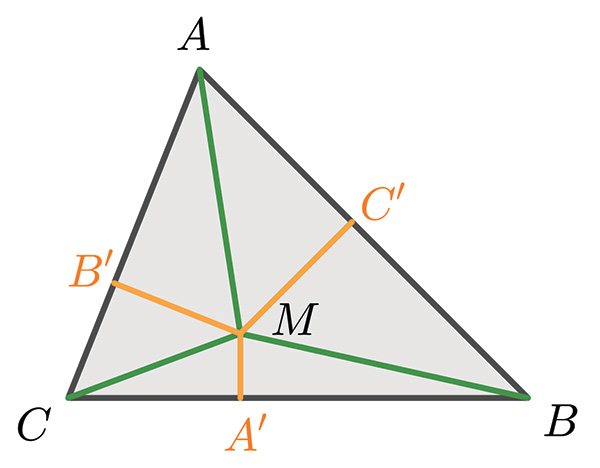
D’après la conjecture d’Erdős, pour n’importe quel point M intérieur au triangle ABC, la moyenne (MA’ + MB’ + MC’)/3 des distances de M aux côtés du triangle est au plus égale à la moitié de la moyenne (MA + MB + MC)/3 des distances aux sommets.
Pour le triangle équilatéral justement, depuis 1649 et le théorème de Viviani on sait que la moyenne des distances aux côtés d’un point intérieur est constante. En prenant pour point intérieur M le centre de gravité des sommets, qui se confond avec l’orthocentre, on vérifie aisément que cette constante est égale au tiers de la hauteur. Un autre résultat du XVIIe siècle nous dit que la moyenne des distances aux sommets atteint son minimum strict en un point appelé point de Fermat (l’unique ... Lire la suite
