
Erdős a proposé de nombreux problèmes concernant la géométrie et, parmi ceux-là, certains possèdent des énoncés relativement simples. En voici deux exemples... mais ce n’est pas pour autant qu’ils sont entièrement résolus.
Le nombre de distances distinctes
Considérez un polygone convexe (c’est-à-dire sans angle rentrant) à neuf sommets, puis calculez les longueurs de ses côtés et de ses diagonales : vous obtenez ainsi un ensemble de nombres positifs. Dans le pire des cas, cet ensemble contient 36 nombres différents (9 côtés et 27 diagonales) et, dans le meilleur des cas, celui de l’ennéagone (polygone à 9 sommets) régulier, seulement 4. Dans l’un de ses derniers articles, daté de 1996, Paul Erdős s’est demandé quelles étaient les configurations des neuf points qui permettaient de n’obtenir que 5 longueurs distinctes et a conclu qu’il n’y avait que deux possibilités : soit les neuf points étaient choisis parmi les sommets d’un décagone (polygone à 10 sommets) régulier, soit ils étaient choisis parmi les sommets d’un hendécagone (polygone à 11 sommets) régulier.
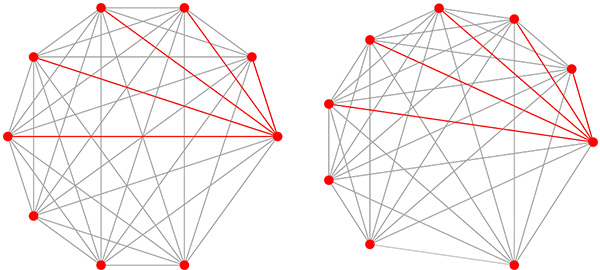
À gauche : les 9 points dans le décagone. À droite : les 9 points dans l’hendécagone.
Le résultat semble anecdotique au regard des recherches ... Lire la suite
