SOLUTION
1. Il faut penser à incliner un carré de huit pieds carrés pour englober douze tours, en plus du donjon.
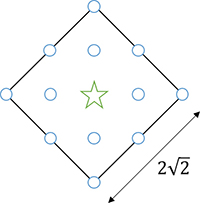
2. Soit d, entier strictement positif, la distance de parcours permettant d’atteindre par les remparts n’importe laquelle des T tours du château.
Montrons que T ≤ 2d(d + 1). La figure (illustration pour d = 4) permet de se convaincre que l’on peut compter toutes les tours atteignables en deux groupes, l’un de d2 et l’autre de (d + 1)2 éléments. En ôtant le donjon, placé dans l’un ou l’autre groupe, on aboutit au résultat.
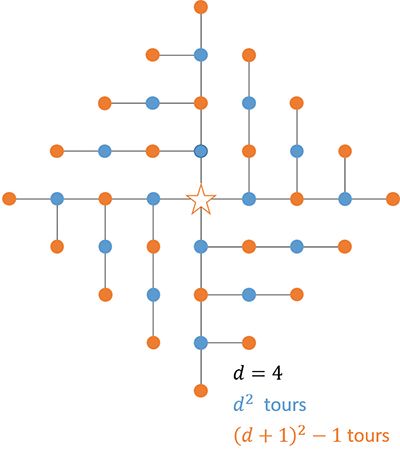
Le nombre minimal de murailles à construire est T. En effet, il ne saurait être inférieur, et la figure montre une façon de ne pas en construire davantage. T / d étant fixé, minimiser T revient à minimiser d.
T / d = 20 ≤ 2d (d + 1) = 9 réalise l’égalité dans la condition précédente. On en déduit que la réponse est cent quatre-vingts murailles.

