Un graphe ayant n sommets numérotés de 1 à n nous est donné. Si le graphe est complet, deux sommets quelconques sont toujours reliés par une arête (ils sont alors adjacents). Un graphe complet à n sommets comprend donc n (n – 1) / 2 arêtes.
Combien d’arbres (en incluant tous ses sommets) peut-on construire sur un graphe complet dont les sommets sont étiquetés ? Un théorème dû au mathématicien britannique Arthur Cayley (1821‒1895) établit que ce nombre est égal à nn–2.
Avec sept sommets, c’est tout !
Considérons un graphe tout simple ne possédant que sept sommets numérotés de 1 à 7. D’après le théorème de Cayley, si le graphe est complet, on peut tracer sur ce graphe pas moins de 75, soit 16 807 arbres différents, ce qui est considérable !
Dans le cas où le graphe n’est pas complet, une généralisation du théorème de Cayley, due au physicien prussien Gustav Kirchhoff (1824‒1887), nous permet de calculer le nombre d’arbres couvrant le graphe. C’est là où le nom de Laplace apparaît.
Supposons que, dans notre graphe, deux sommets quelconques soient adjacents si, et seulement si, la différence de leurs numéros, prise en valeur absolue, est égale à 3 ou à 4. Pour appliquer la méthode de Kirchhoff, on fera appel à deux matrices : la matrice d’adjacence A et la matrice des degrés D.
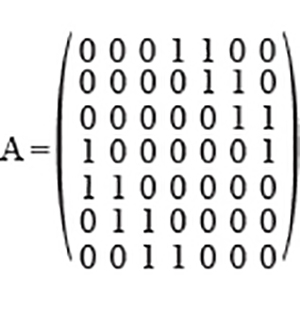
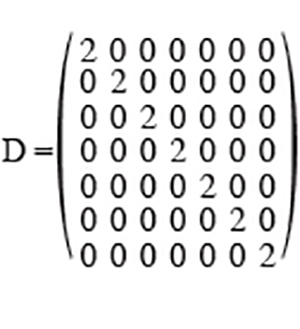
Dans A, le coefficient ai,j vaut 1 si |i – j| = 3 ou 4, et 0 sinon. Dans D, on indique sur la diagonale les degrés de chaque sommet, c’est-à-dire le nombre de sommets auquel il est relié par une arête. Enfin, on construit la matrice laplacienne L, égale à D – A.

D’après la méthode de Kirchhoff, le nombre d’arbres couvrant notre graphe est égal à n’importe quel cofacteur de la matrice laplacienne. Concrètement, on supprime une ligne et une colonne de cette matrice, puis on calcule le déterminant de la matrice résultante. En effectuant ce calcul avec notre matrice laplacienne, on obtient un résultat égal à 7.
Ceci s’explique aisément. En effet, le graphe est un simple circuit reliant les nombres de 1 à 7.
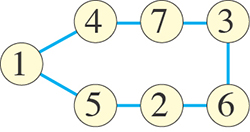
Pour obtenir un arbre, il suffit de supprimer une arête, et on peut le faire de sept façons.
Si l’on considère les nombres de 1 à 8, avec la même condition d’adjacence (valeur absolue de la différence égale à 3 ou 4), combien d’arbres couvriront le graphe correspondant ?

