Considérons une série de timbres imprimés sur une bande de papier dont le verso est gommé, c’est-à-dire enduit d’une colle sèche qu’il suffit d’humidifier pour coller le ou les timbres sur une enveloppe. Les séparations entre les timbres sont perforées de petits trous, de façon à pouvoir facilement les séparer sans déchirer les timbres.

Voici la question qui nous intéresse : de combien de manières peut-on plier cette bande de timbres de façon à tous les replier sur un seul d’entre eux, les pliages devant se faire uniquement selon les lignes perforées ?
Le pliage doit être réalisé de telle sorte que le timbre numéro 1 ait sa face imprimée au-dessus et que les perforations entre les timbres 1 et 2 soient situées à droite, ce qui élimine un certain nombre de cas obtenus par des symétries.
Le mathématicien François Édouard Anatole Lucas (1842‒1891) énonce cette question dans sa Théorie des nombres publiée en 1891 (Gauthier-Villars), en citant Émile Michel Hyacinthe Lemoine (1840‒1912) comme étant à l’origine du problème. André Sainte-Laguë (1882‒1950) étudiera ce problème dans un chapitre de son livre Avec des nombres et des lignes (Vuibert, 1937).
Commençons notre collection...
Pour nous échauffer, démarrons avec une bande de deux timbres. Il n’y a que deux façons de plier cette bande en respectant les conditions sur le timbre numéro 1. Sur le schéma, les faces imprimées apparaissent en couleur, les faces gommées en noir et les perforations entre les timbres en pointillés.
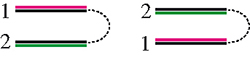
Passons à une bande de trois timbres. On dénombre six pliages différents, qui correspondent aux six permutations d’un ensemble à trois éléments : (1, 2, 3), (1, 3, 2),
(2, 1, 3), (2, 3, 1), (3, 1, 2) et (3, 2, 1).
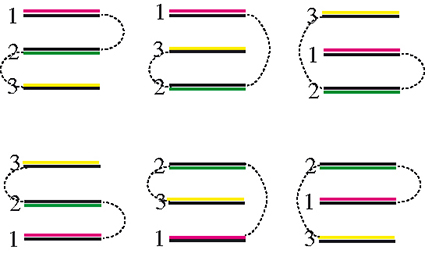
Les choses se gâtent en passant à une bande de quatre timbres. En effet, il existe vingt-quatre permutations d’un ensemble à quatre éléments. Mais si vous essayez de dénombrer tous les pliages possibles d’une bande de quatre timbres, toujours en respectant les conditions sur le premier timbre, vous n’en trouverez pas 24, mais seulement 16. Pourquoi ?
La raison en est que certaines permutations conduisent à des pliages impossibles à réaliser physiquement sans qu’un timbre ne passe à travers une ligne de perforations.
1. Sur ces vingt-quatre permutations, quelle sont celles qu’il est impossible de réaliser par pliage ?
(1, 2, 3, 4), (1, 3, 2, 4), (2, 1, 3, 4), (2, 3, 1, 4), (3, 1, 2, 4),
(3, 2, 1, 4), (1, 2, 4, 3), (1, 3, 4, 2), (2, 1, 4, 3), (2, 3, 4, 1),
(3, 1, 4, 2), (3, 2, 4, 1), (1, 4, 2, 3), (1, 4, 3, 2), (2, 4, 1, 3),
(2, 4, 3, 1), (3, 4, 1, 2), (3, 4, 2, 1), (4, 1, 2, 3), (4, 1, 3, 2),
(4, 2, 1, 3), (4, 2, 3, 1), (4, 3, 1, 2), (4, 3, 2, 1).
Dans un pliage, quels timbres auront leur face imprimée au-dessus ?
Il est facile de constater que si l’on impose au premier d’avoir sa face imprimée au-dessus, il en sera de même pour tous les timbres de numéro impair, et que les timbres portant un numéro pair auront leur face gommée au-dessus.
Si aucune formule générale n’est connue, André Saint-Laguë a néanmoins trouvé une relation intéressante. Si A(n) est le nombre de pliages faisant apparaître le timbre numéro 1 sur le dessus, le nombre total de pliages réalisables est égal à nA(n).
2. Combien existe-t-il de pliages d’une bande de cinq timbres ?

