En forêt de Mathagonie, un circuit pédestre a été tracé selon un octogone ABCDEFGH qui a la forme d’un heaume de chevalier.
Les points A, C, G et E sont alignés, ainsi que les points E, F et H.
Le triangle ABC est isocèle de sommet A, et le triangle DEF est équilatéral.
E est à égale distance de A et de B.
L’angle vaut 30°, les angles
et
valent 80°, les angles
et
valent 90°.
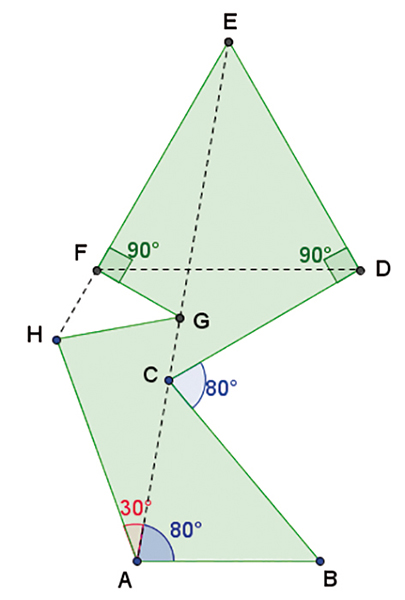
Alice et Bob partent en même temps, l’une du point A et l’autre du point B, pour effectuer respectivement les trajets AHGFE et BCDE. Ils arrivent ensemble au point E. Alice a marché à 6 km/h.
Quelle a été la vitesse de marche de Bob ?
Si nécessaire, on utilisera 0,985 pour sin (80°).

