Quelles sont les propriétés mathématiques des formats normalisés de notre quotidien, qui sont utilisés dans la photographie, l’édition, la peinture ou l’architecture ?
Le b.a.-ba des formats A et B
La définition du format A4 repose sur une norme de l’Afnor (Association française de normalisation). Cette norme datant de 1967 définit un format A0 comme étant un rectangle d’un mètre carré qui soit divisible en deux rectangles égaux (rectangles A1) qui lui soient semblables.

Un calcul simple montre que la longueur d’un tel rectangle doit être égale à la largeur multipliée par (environ 1,414). Une feuille de papier au format A0 aura donc une longueur (en mètres) égale à
et une largeur égale à
La norme arrondit ces dimensions respectives à 1,189 m et 0,841 m.
En divisant la feuille en deux, puis en quatre, en huit…, on définit les formats A1, A2, A3, A4…, tous semblables les uns aux autres, aux arrondis près.
La norme ISO 216 de l’International Standards Organization définit également des formats B0, B1, B2…, qui possèdent les mêmes propriétés, le format B0 ayant une largeur d’un mètre et une longueur valant 1,414 mètre. Chaque format Bn contient donc le format An et est contenu dans le format A(n–1).
Prenez maintenant une photo rectangulaire, de dimensions quelconques. Adjoignez-lui un carré de façon à obtenir un nouveau rectangle plus grand. Répétez cette opération avec le rectangle obtenu, et continuez ainsi de façon à obtenir des rectangles de plus en plus grands.

L’image initiale ayant des dimensions quelconques, vous aurez peu de chances d’obtenir des formats standards, mais les formats successifs vont « se rapprocher peu à peu » d’un format bien particulier.
Soient a et b la largeur et la longueur de la photo de départ.
Les rapports des rectangles successifs produisent cette suite :
Par construction, les coefficients successifs de a et de b (tant au numérateur qu’au dénominateur) sont les nombres de la célèbre suite de Fibonacci (Fn)n ≥ 0, à savoir 1, 1, 2, 3, 5, 8…, où Fn+2 = Fn+1 + Fn. Or, lorsque n tend vers l’infini, le rapport Fn+1/Fn tend vers le nombre d’or , soit environ 1,618.
Notre rapport tendra donc vers l’inverse du nombre d’or
, égal à
, qui vaut environ 0,618.
De même, si, dans un rectangle, on découpe un carré dont le côté correspond à la largeur du rectangle et que le rectangle restant est semblable au rectangle initial, alors le rapport du rectangle initial est égal au nombre d’or.
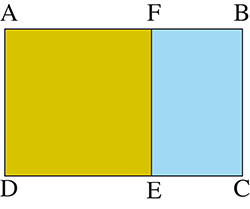
Si AFED est un carré et si AB / BC = BC / EC, alors AB / BC =  .
.
En découpant deux carrés ou plus
Si la longueur du rectangle est comprise entre le double et le triple de la largeur, on peut découper deux carrés ayant pour côté la largeur du rectangle, et trois carrés lorsque la longueur du rectangle initial est comprise entre le triple et le quadruple de la largeur.
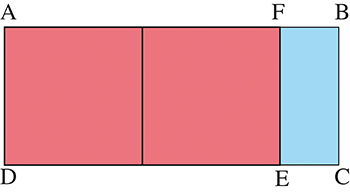

1. Quel doit être le rapport largeur/longueur du rectangle ABCD pour que, une fois les deux carrés ôtés, le rectangle restant BCEF soit semblable au grand rectangle initial ?
2. Même question lorsque l’on peut ôter trois carrés du rectangle initial.
3. Généraliser au cas où on peut ôter n carrés (n > 3) du rectangle initial.

