
Cauchy a démontré que tous les polyèdres convexes sont rigides (voir article « Premières découvertes »), c’est-à-dire que si l’on construit un polyèdre convexe dont les faces sont des tôles d’acier et les arêtes des charnières alors il est impossible de modifier la forme de l’objet, tout comme si les charnières étaient soudées. C’est ainsi qu’un échafaudage, constitué de polyèdres convexes, est stable !
Dans le théorème de Cauchy il y a toutefois une hypothèse très contraignante : la convexité du solide. Sans surprise, la question s’est alors posée de savoir dans quelle mesure on pouvait supprimer cette hypothèse. À l’époque de Cauchy tous les polyèdres connus étaient rigides, y avait-il donc un théorème là-dessous ? Cauchy lui-même fit quelques recherches, mais ne parvint pas à conclure.
Contre-exemples partiels
En 1898, Raoul Bricard (1870-1943) est le premier à exhiber un polyèdre à la fois non convexe et flexible : l’octaèdre de Bricard. Si le polyèdre est matérialisé par des barres articulées aux sommets alors le polyèdre est flexible. Seule petite déception : ses faces s’intersectent entre elles. Bricard découvre ensuite un second octaèdre flexible, mais toujours avec des faces qui se croisent.
En 1900, Max Brückner, dans sa somme intitulée Vielecke und Vielflache, décrit des anneaux de tétraèdres, une idée qui sera redécouverte plusieurs fois par la suite. Il s’agit de tétraèdres réguliers reliés entre eux par leurs arêtes. Lorsqu’ils sont au moins 6, la chaîne peut se refermer sur elle-même et autoriser un mouvement. À partir de 8, l’anneau peut même tourner indéfiniment sur lui-même. Mais peut-on encore parler de polyèdre quand ses parties constitutives se tiennent par une arête ?…
Les tribulations de Connelly
Au début des années 1970, le mathématicien américain Herman Gluck démontre, que presque tous les polyèdres non convexes sont rigides, en un sens mathématique précis. En d’autres termes, un polyèdre non convexe choisi « au hasard » a toutes les chances d’être rigide. Toutefois, cela ne suffit pas pour dire qu’il n’y aurait aucune exception. Le Canadien Robert Connelly se met alors à la recherche de celle-ci. Il semble proche d’une solution lorsqu’au congrès de topologie de 1975 de l’université de Cornell, il entend parler d’un jeune confrère qui serait sur le point de conclure lui aussi. En remontant les rumeurs à la source, il découvre heureusement que ce jeune confrère… n’est autre que lui-même ! Et finalement, deux ans plus tard, Connelly dévoile un polyèdre non convexe et flexible, assez compliqué, mais sans auto-intersections. Il possède 18 sommets et est isomorphe à la sphère. Cette fois, l’affaire est définitivement close : le théorème de rigidité est faux pour les polyèdres non convexes.
Par la suite, Nicolaas Kuiper et Pierre Deligne simplifient l’exemple de Connelly, obtenant un polyèdre flexible fait de 18 faces et 11 sommets. Enfin, Klauss Stephen, à partir de considérations différentes, construit un nouvel exemple avec 14 faces triangulaires et 9 sommets. Par ailleurs, le mathématicien russe Maksimov montrera qu’un polyèdre flexible, isomorphe à la sphère, et constitué de triangles ne peut pas avoir moins de 9 sommets : le polyèdre de Stephen est donc un exemple avec le moins de sommets possibles.

Le polyèdre de Stephen.
La flexibilité notable (sans être démesurée) du polyèdre de Stephen
en fait un objet qui excite facilement la curiosité.

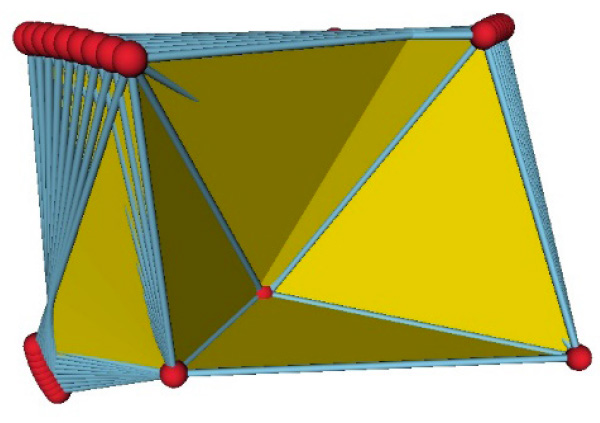
Les débattements (positions extrêmes) du polyèdre de Stephen,
vus sous deux angles.
Des polyèdres aux flexaèdres
La légende veut que Sullivan ait soufflé la fumée de sa cigarette dans le polyèdre de Connelly tout en manœuvrant celui-ci, et qu’il remarqua que la fumée ne sortait pas. De quoi penser que le polyèdre se déformait en gardant un volume constant ! Voilà bien peut-être le seul usage positif qui ait jamais été fait de la consommation de tabac… Après vérifications par des calculs aussi longs que pénibles, un théorème est établi : tous les polyèdres flexibles connus à l’époque gardent un volume constant quand on les déforme. Mais est-ce une propriété générale ?
La réponse, affirmative, tombe en 1997 : c’est le théorème du soufflet, obtenu par R. Connelly, I. Sabitov et A. Walz. La démonstration s’appuie sur une généralisation d’un très vieux résultat dû à Héron d’Alexandrie, qui a un air de famille avec le théorème du soufflet : la surface S d’un triangle de côtés a, b et c est donnée par la formule
où p est le demi périmètre du triangle (c’est-à-dire p = (a + b + c) / 2 ). Une extension de ce résultat, nécessaire pour le théorème du soufflet, consiste à démontrer que le carré du volume d’un polyèdre est solution d’une équation de degré n dont les coefficients ne dépendent que des longueurs des arêtes. Une fois obtenu ce résultat, il s’ensuit que le volume d’un polyèdre dont les longueurs des arêtes sont données ne peut prendre que n valeurs distinctes (car une équation de degré n ne peut avoir qu’au plus n solutions). En pratique la valeur de n est très grande, toujours est-il que le volume du polyèdre flexible correspondant ne peut donc prendre qu’un nombre fini de valeurs. Puisque le volume varie continûment lors de la déformation du polyèdre, pour ne pas décrire une infinité de valeurs il doit donc rester figé à une valeur unique.
Les polyèdres flexibles sont appelés flexaèdres, leur existence posent de nombreuses questions nouvelles. Cauchy n’aurait pas disposé de l’arsenal théorique nécessaire pour les étudier, son mémoire de 1812 n’en a pas moins été fondateur d’un domaine qui continue aujourd’hui à se développer.



