
Les tous premiers résultats mathématiques de Cauchy paraissent en février 1811 dans le Journal de l’École polytechnique. Il s’agit d’une réponse à une question sur les polyèdres, posée par Louis Poinsot (1777-1859), un mathématicien de douze ans son aîné.
Comme on le sait, il n’existe que cinq polyèdres dits réguliers, c’est-à-dire des solides convexes dont les faces sont des polygones réguliers (c’est-à-dire de côtés égaux faisant entre eux des angles égaux) tous identiques. Ce sont, par ordre croissant du nombre de faces : le tétraèdre (4 faces triangulaires), le cube (6 faces carrées), l’octaèdre (8 faces triangulaires), le dodécaèdre (12 faces pentagonales) et l’icosaèdre (20 faces triangulaires). Avec seulement cinq polyèdres réguliers possibles, on est bien loin de l’infinité des polygones réguliers. Également appelés solides de Platon, ces polyèdres ont été étudiés et généralisés depuis l’Antiquité, notamment par Kepler.

Les solides de Platon : octaèdre, tétraèdre, cube, icosaèdre, dodécaèdre.
Poinsot, l’éclaireur
L’une des façons de généraliser les polyèdres réguliers pour créer de nouvelles formes consiste à renoncer à la condition de convexité, implicite chez les Grecs. C’est ce que choisit de faire Poinsot en partant à la chasse aux polyèdres en 1809. Il découvre ainsi le grand icosaèdre, un solide non convexe composé de 20 triangles qui s’entrecroisent, construit à partir de l’icosaèdre ordinaire (voir encadré ci-dessous).
Le grand icosaèdre
On part d’un icosaèdre ordinaire, polyèdre régulier convexe à 20 faces triangulaires, 12 sommets et 30 arêtes. Plaçons-nous à un sommet S. Comme on le voit sur le dessin de gauche, ce sommet a 5 voisins immédiats. Il a aussi un sommet qui lui est opposé, et les 5 derniers sommets sont à une même distance intermédiaire de S.
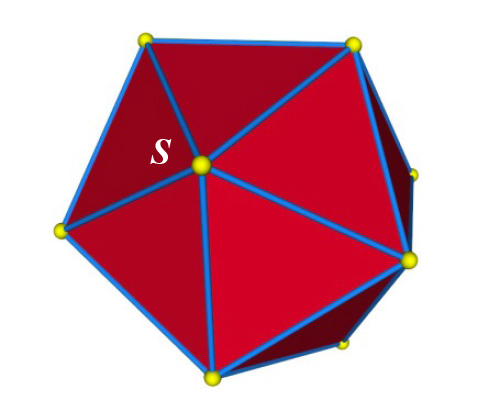
Ces sommets à distance intermédiaire permettent de définir des triangles équilatéraux.
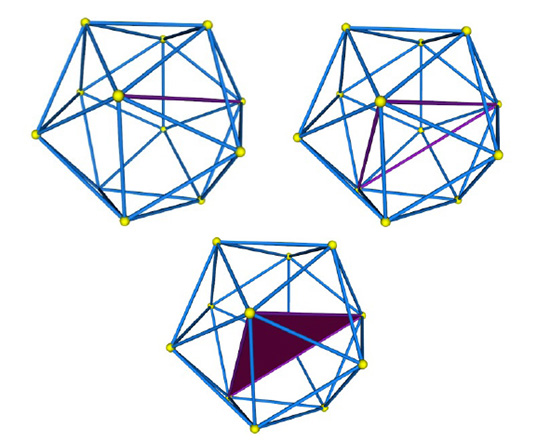
Il y a en tout 30 segments à tirer entre tous les sommets à distance intermédiaire, qui définissent ainsi 20 triangles équilatéraux qui sont les faces du nouveau solide.
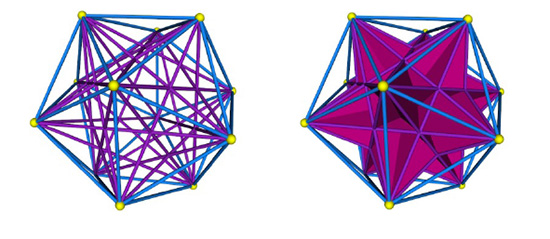
Ainsi apparaît le grand icosaèdre :

Il découvre aussi le grand dodécaèdre, composé de 12 pentagones, qui s’entrecroisent également (voir encadré ci-dessous).
Le grand dodécaèdre
Solide non convexe constitué de douze pentagones, le grand dodécaèdre se construit lui aussi à partir d’un icosaèdre. Les cinq sommets voisins d’un sommet donné sont coplanaires et forment un pentagone régulier. En matérialisant les douze pentagones de ce type, on obtient le grand dodécaèdre.

Poinsot n’en reste pas là. Ayant ainsi trouvé de nouveaux polyèdres dont les faces sont des polygones convexes, il s’intéresse aux assemblages d’étoiles. Ce faisant, il redécouvre le petit et le grand dodécaèdre étoilé, des solides déjà imaginés par Kepler.
Dans son mémoire publié dans le Journal de l’École polytechnique, Poinsot pose alors la question suivante : « Est-il possible qu’il existe des polyèdres réguliers dont le nombre de faces ne serait pas un de ceux-ci, 4, 6, 8, 12, 20 ? Voilà une question qui mériterait d’être approfondie, et qu’il ne paraît pas facile de résoudre en toute rigueur. »
Les choses en sont là lorsque, deux ans plus tard et sur les conseils de Lagrange, Cauchy entre en scène. Pour répondre à la question de Poinsot, il commence par observer, comme Kepler avant lui, qu’une étoile, qui n’est autre qu’un polygone régulier non convexe, peut s’obtenir en prolongeant les côtés des polygones réguliers. Certes, quand on prolonge les côtés d’un triangle, il ne se passe rien…
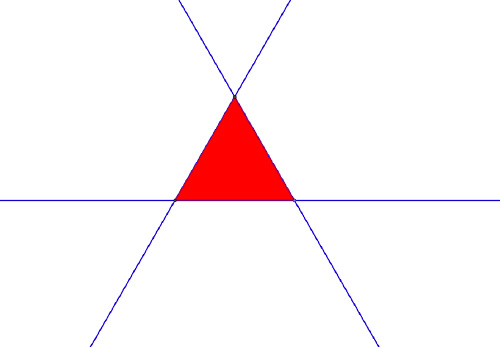
… pas plus qu’en prolongeant les côté d’un carré.
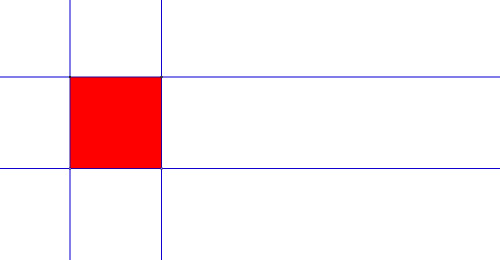
Avec le pentagone, en revanche, les droites se recoupent pour former une étoile à 5 branches (ou pentagramme).
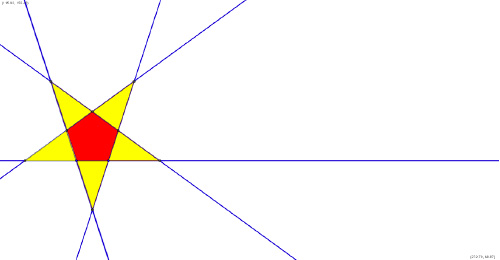
Avec l’hexagone régulier on obtient une étoile faite de deux triangles équilatéraux.
.jpg)
L’heptagone, quant à lui, donne naissance à deux étoiles (ici, jaune et orange).
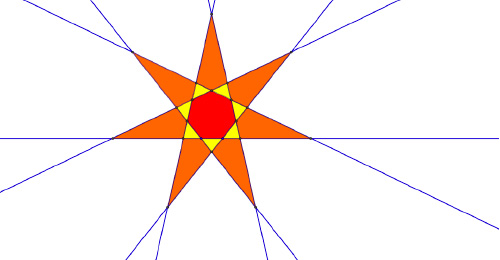
Cauchy pense alors que les polyèdres étoilés s’obtiennent de façon analogue, en prolongeant les arêtes et les faces de polyèdres réguliers. Il fait l’expérience de pensée de se mettre au centre d’un polyèdre régulier étoilé. Vus de ce centre, les plans des faces de ce polyèdre forment un polyèdre convexe. Celui-ci, pour des raisons de symétrie longuement détaillées par Cauchy, est nécessairement régulier. Il ne reste donc qu’à étudier ce qui se passe pour chacun des cinq solides réguliers.
Pour le tétraèdre, les arêtes prolongées ne se recoupent pas.
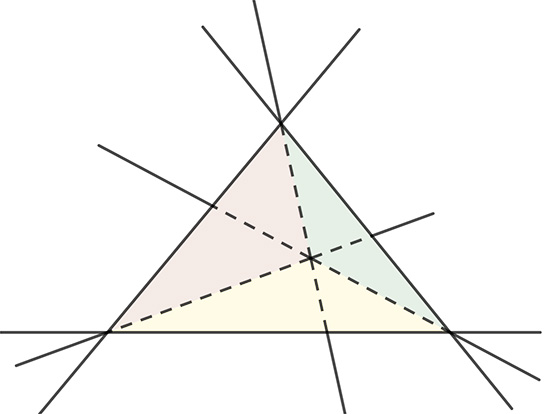
Il en est de même pour le cube.
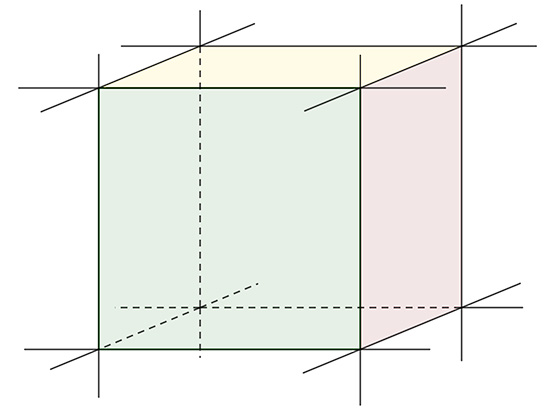
Pour l’octaèdre, les arêtes ne se recoupent pas mais les plans des faces, eux, se recoupent pour former des pyramides tétraédriques sur chaque face. Le nouveau solide résultant est constitué de deux tétraèdres réguliers imbriqués, qui n’est pas à proprement parler un solide régulier étoilé. Il faut donc ajouter la condition qu’un sous-ensemble du solide ne soit pas un solide régulier.
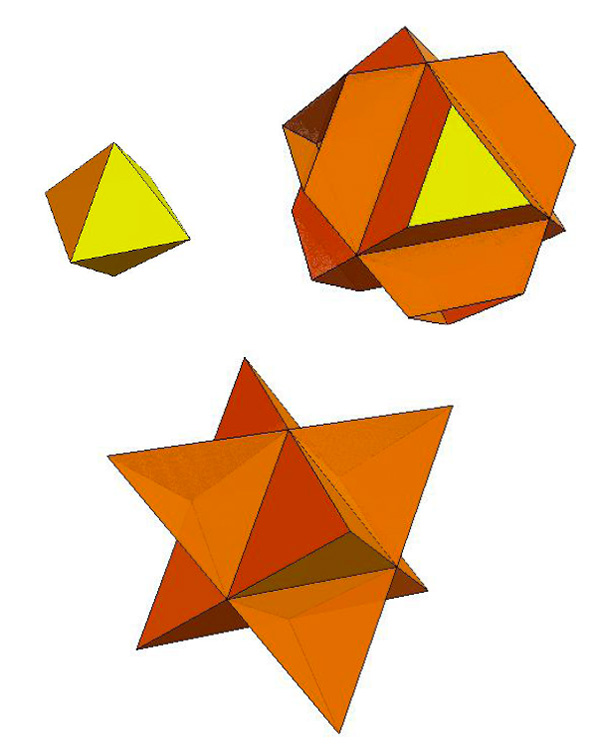
Le cas du dodécaèdre est plus fécond. En prolongeant les arêtes, les pentagones se transforment en pentagrammes, leur réunion conduit au petit dodécaèdre étoilé.
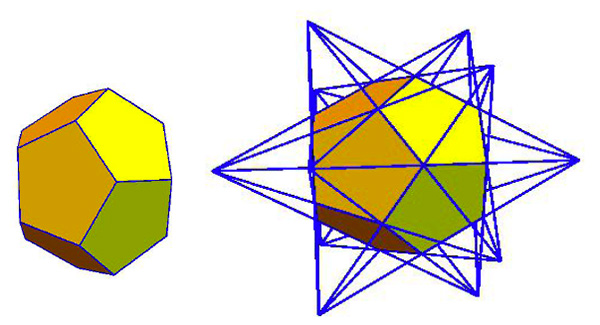
Si on choisit plutôt de prolonger les faces, on obtient d’abord un petit dodécaèdre étoilé…
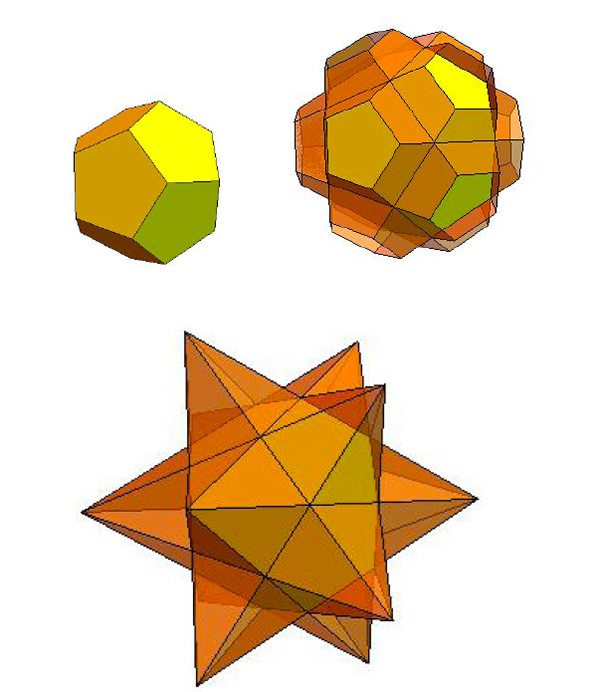
… puis un grand dodécaèdre…
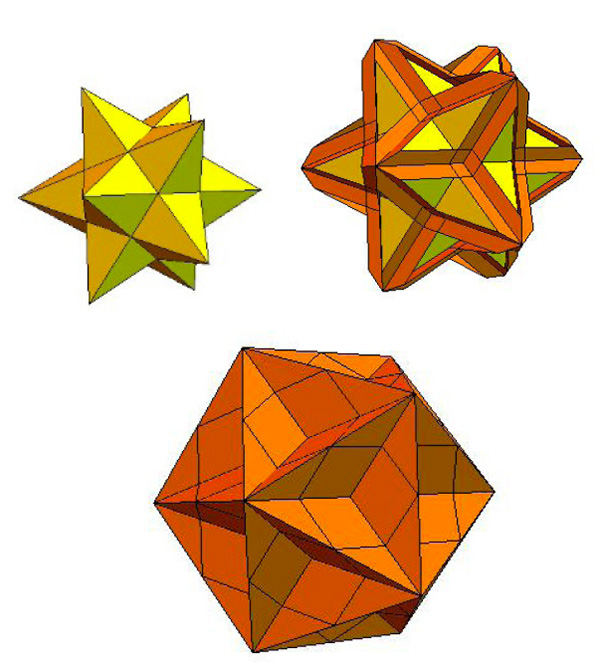
… et enfin un grand dodécaèdre étoilé.
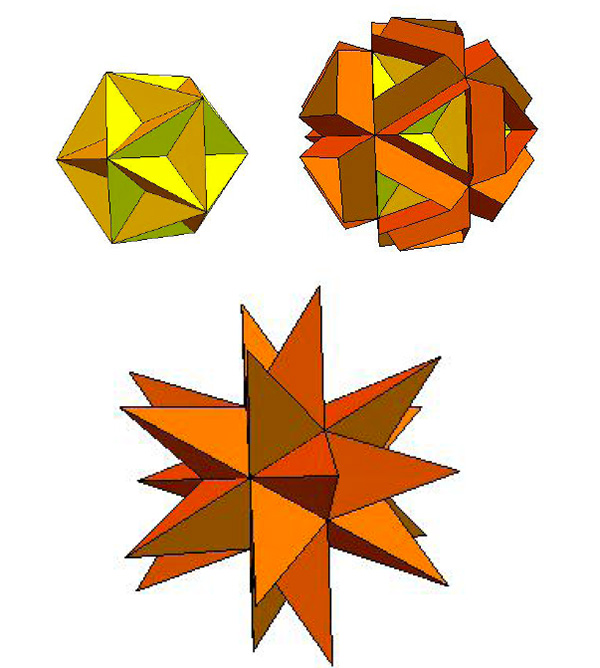
Reste le cas de l’icosaèdre. La prolongation de ses arêtes redonne le grand dodécaèdre étoilé…
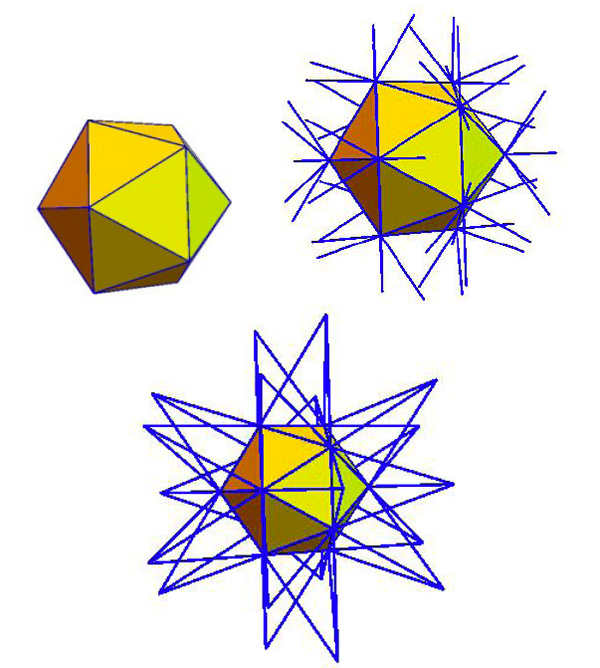
… tandis que le prolongement de ses faces conduit au grand icosaèdre.
Les quatre polyèdres étoilés ainsi construits sont appelés les étoiles de Poinsot-Kepler, mais c’est bel et bien Cauchy qui a démontré qu’il n’existe que ces quatre-là. Un siècle plus tard, le géomètre britanique Harold Coxeter (1907-2003) ira encore plus loin en démontrant que les plans des faces de l’icosaèdre produisent des cellules de l’espace qui peuvent conduire à 59 étoiles, dont une seule est régulière.

Sculpture d'un dodécaèdre étoilé d'après un dessin d'Escher,
université de Twente, Pays-Bas.
références
• Recherches sur les polyèdres,
Augustin Cauchy,
Journal de l’École polytechnique, seizième cahier, tome IX,
mai 1813.
• Mémoires sur les polygones et les polyèdres, Louis Poinsot,
Journal de l’École polytechnique, dixième cahier, tome IV, novembre 1810.
• Sur les polyèdres étoilés d’après M. Cauchy, Olry Terquem,
Nouvelles annales de mathématiques 1ère série, tome 8, 1849.


