
Érudit, mathématicien, astronome, Francesco Maurolico reste connu pour ses travaux en géométrie, en optique, sur les coniques, en mécanique ou encore en musique. Il a traduit du grec des œuvres d’Euclide, d’Apollonius de Perge et d’Archimède. En 1572, il observe le phénomène de « nouvelle étoile » dans la constellation de Cassiopée, implosion d’étoile devenue, depuis, la « supernova de 1572 ».

Francesco Maurolico (1494‒1575).
Deux livres sur les nombres
Parmi ses écrits mathématiques (en latin), on distingue les Opuscula mathematica, publiés en 1575, peu après son décès, avec en supplément les Arithmeticorum libri duo, rédigés dès 1557, dont l’intitulé complet indique l’ambition de l’auteur : « Deux livres d’arithmétique, publiés pour la première fois. Avec toutes choses notables. Une liste très copieuse. »
Maurolico déploie considérablement le regard sur les nombres figurés. Pour quelle raison ? Il s’en explique : « Non seulement pour démontrer plus facilement ce qui a été obscurément transmis par d’autres, mais aussi pour compléter ce qui a été omis. » Il cite des prédécesseurs anciens – Nicomaque de Gérase II e siècle), Jamblique (III e siècle), Boèce (IV e et Ve siècles) – ou plus récents, comme Jordanus de Nemore au XIII e siècle.
Le livre I (seul présenté ici) comprend une première partie pour les nombres figurés « de première espèce » : ce sont les lignes, à savoir les racines (les entiers naturels à partir de 1 ; la racine est le nombre de points sur le côté d’une représentation d’un nombre figuré), les impairs, les pairs, puis les polygones (triangles, carrés, pentagones, hexagones…) ; les pyramides (triangulaires, carrées, pentagonales…) ; et les colonnes (triangulaires, carrées, pentagonales…). Par pyramide, on entend un empilement de polygones de même nombre de côtés à partir du premier (l’unité) ; pour colonne, comprendre un empilement du même polygone autant de fois que la racine (ce sont des prismes). Dans une seconde partie, on trouve l’exposé analogue pour les nombres figurés « centrés », puis l’introduction et l’étude de solides pour des nombres figurés centrés spatiaux à partir des cinq solides de Platon.
Au long des quatre-vingt-deux pages de ce livre I, Maurolico fait très peu de figures ! Son emploi des nombres figurés apparaît plus mental que visuel. Il n’y a pas non plus de formules. S’il énonce que le produit de la racine et de la racine suivante vaut le double du nombre triangulaire, ce n’est pas notre n(n + 1) = 2(1 + 2 +… + n).
Au-delà du triangle et du carré, Maurolico suit ce qu’ont fait Boèce et Jordanus avant lui, en définissant les nombres polygones par adjonction d’un carré et de triangles. Ainsi, le pentagone est un carré assemblé avec un triangle de racine précédente, l’hexagone est carré et deux triangles de racine précédente. Ce procédé a sa limite : comment représenter un ennéagone avec un carré et cinq triangles précédents ?

Représentations de Maurolico.

Représentations par accroissement arithmétique.
Le gnomon comme fil conducteur
Le terme « gnomon » a des emplois divers. En astronomie, c’est l’axe du cadran solaire (la gnomonique est d’ailleurs la science des cadrans solaires). En géométrie, c’est une figure géométrique qui, ajoutée à une figure donnée, la transforme en une figure semblable à la première. Ce sens peut être appliqué aux nombres figurés :
- le polygone est gnomon de pyramide, par définition ;
- la racine est gnomon du nombre triangulaire. L’entier 15, égal à 1 + 2 + 3 + 4 + 5, est le cinquième nombre triangulaire, de gnomon 6 car 15 + 6 = 21, sixième nombre triangulaire.
- le gnomon le plus remarqué est sans doute le nombre impair. Étant donné un carré, 36 par exemple (le sixième), l’impair 13 (le septième) fait que 36 + 13 = 49, qui est le septième carré.

Le grand intérêt des nombres figurés est qu’ils montrent, visuellement, qu’un nombre triangulaire est somme des premiers entiers, qu’un nombre carré est somme de premiers impairs.
L’une des propositions du livre I énonce qu’il existe de nombreux carrés qui, combinés, forment un carré. Maurolico propose deux approches. La première part de l’observation que la différence de deux carrés consécutifs est un nombre impair ; il suffit donc de chercher des nombres impairs qui soient carrés pour obtenir des triplets pythagoriciens. Son exemple est le suivant : 9 est impair, gnomon de 16 à 25. Ce 25, lui-même impair, le treizième, carré, peut engendrer un nouveau triplet pythagoricien : 122 + 25 = 132 (voir notre dossier « Les triplets pythagoriciens », Tangente 212, 2023).
Son autre approche, plus « euclidienne », est une conséquence de la proposition 5 du livre II des Éléments d’Euclide.
En termes modernes : pour deux nombres a et b, on a
En proposant deux entiers de même parité dont le produit est un carré, Maurolico obtient un triplet pythagoricien ; avec a = 9 et b = 25, il trouve 15 2 + 8 2 = 17 2.
Dites-le avec des cubes
L’ordonnancement de l’exposé présente une exception ! Dans son étude des polygones simples, Maurolico est conduit à considérer le nombre composé de l’unité et de six triangles de même racine, qui est l’hexagone centré de racine suivante.Il montre que l’hexagone centré est gnomon du cube.
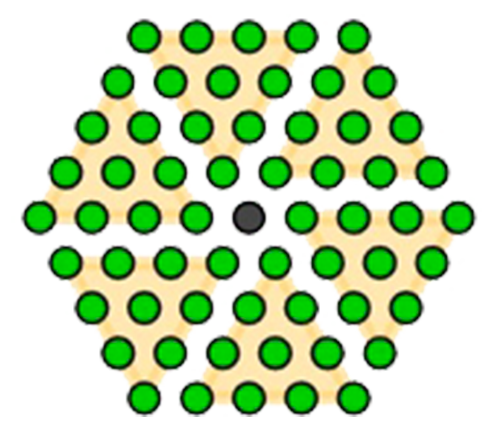
Cinquième hexagonal centré : 61.
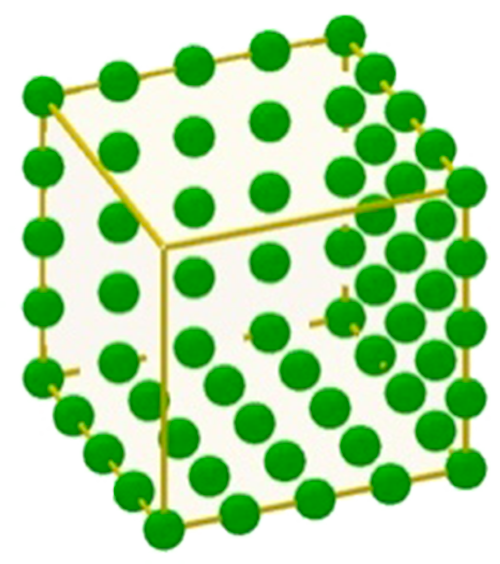
Du quatrième cube au cinquième.
Il démontre ensuite : « Chaque cube joint au carré du triangle précédent forme le carré du triangle collatéral. » Maurolico prouve ce résultat, déjà connu (au moins depuis Nicomaque de Gérase) : la somme des cubes et le carré du triangle. Il s’agit de gnomon du carré d’un nombre triangulaire.
Illustrons par un exemple : le sixième cube est 216, le cinquième triangle est 15, de carré 225 ; leur somme, 441, est carré de 21, le sixième triangle. Ajouter 63 au carré du cinquième triangle donne le carré du sixième. Entendue dans une acception générale, la notion de gnomon peut être de plus en plus raffinée !
Des nombres figurés plus élaborés
Partant des cinq solides réguliers de Platon (le tétraèdre, l’octaèdre, le cube, l’icosaèdre et le dodécaèdre), Maurolico définit des nombres figurés solides. Les trois premiers s’inspirent des nombres figurés simples : le tétraèdre comme pyramide triangulaire, empilement (somme) de triangles ; l’octaèdre consiste en un assemblage de deux pyramides carrées successives, comme le carré l’est de deux triangles ; le cube est colonne, assemblage de carrés de même racine au nombre de cette racine.
Des nombres figurés d’un deuxième genre, les centrés, ont été évoqués par Jordanus ; Maurolico les reprend. Comme pour l’hexagone, les polygones centrés sont assemblage de l’unité et d’autant de triangles précédents qu’il y a de côtés. De la sorte, le carré centré est somme du carré simple et de son précédent ; le polygone centré est assemblage du polygone simple de même racine et du carré précédent ; l’octogone est carré de l’impair.
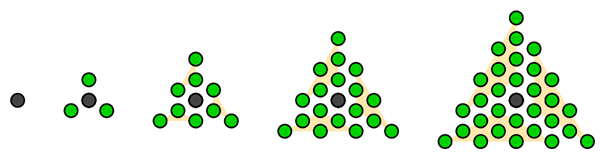
Triangles centrés : 1, 4, 10, 19, 31, 46…
Pyramides triangulaires centrées : 1, 5, 15, 34, 65, 111…
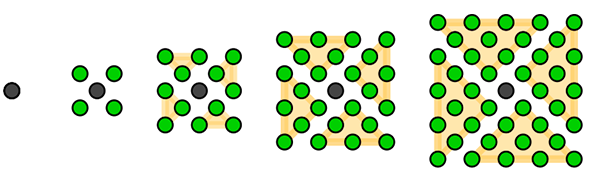
Carrés centrés : 1, 5, 13, 25, 41, 61…
Le carré centré est somme de deux carrés successifs.
Pyramides carrées centrées : 1, 6, 19, 44, 85, 146…
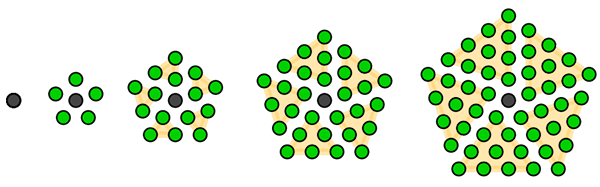
Pentagones centrés : 1, 6, 16, 31, 51, 76…
Pyramides pentagonales centrées : 1, 7, 23, 54, 105, 181…
Les pyramides centrées sont un empilement (ou somme) de polygones centrés de même nombre de côtés à partir du premier (l’unité) ; les colonnes centrées sont un empilement (ou somme) du même polygone centré, autant de fois que la racine.
Ces nombres figurés centrés permettent de considérer d’autres solides, en observant qu’un nombre polygone centré peut être expliqué par une décomposition en formes plus élémentaires, comme pour l’hexagone centré. L’icosaèdre possède douze sommets, trente arêtes et vingt faces triangulaires. Considérant le centre en tant qu’unité, on forme le nombre figuré en assemblant avec l’unité, douze racines précédentes (« rayons »), trente triangles anté-précédents, vingt pyramides triangulaires centrées précédentes. C’est un « éclaté » qui rend compte du nombre figuré.
De même, le dodécaèdre est obtenu avec l’unité, vingt racines précédentes, trente triangles anté-précédents et douze pyramides pentagonales centrées précédentes.
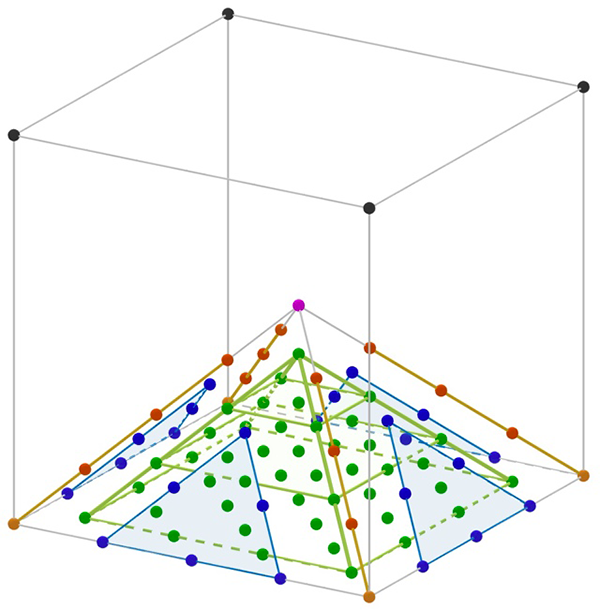
Base de l’éclaté du cinquième cube centré.
Cubes centrés : 1, 15, 65, 175, 369.
Cela conduit Maurolico à reconsidérer les trois premiers solides, pour un nouveau type, les solides centrés :
- le tétraèdre centré : l’unité, quatre racines précédentes, quatre triangles anté-précédents, quatre pyramides centrées précédentes ;
- le cube centré : l’unité, huit racines précédentes, douze triangles anté-précédents, six pyramides carrées centrées précédentes ;
- l’octaèdre centré : l’unité, six racines précédentes, douze triangles anté-précédents, huit pyramides triangulaires centrées précédentes.
Ce faisant, l’auteur a le sentiment d’inventer : « Et que vous, lecteur très perspicace, ne vous lassiez pas de considérer les choses qui se rapportent principalement à de telles formes numériques, omises par d’autres, et à la perfection de la spéculation arithmétique. Car vous en saurez les propriétés qui méritent d’être notées, et qui ne sont données qu’aux esprits curieux. »
Des nombres solides égaux
Les compositions de Maurolico, par leurs définitions, inspirent des comparaisons. S’agit-il de cinq familles nouvelles ? Non, deux propriétés identifient d’une part le cube et l’octaèdre, d’autre part le dodécaèdre et l’icosaèdre.
|
|
Racines |
Triangles |
Pyramides |
|
Cube |
8 |
12 |
six carrées |
|
Octaèdre |
6 |
12 |
huit |
Comparons les pyramides triangulaires et carrées. Elles sont empilements, respectivement, de triangles centrés, de carrés centrés. Commençons par comparer ces couches composantes. Maurolico énonce que trois carrés centrés et quatre unités valent quatre triangles centrés et trois unités. Il suffit d’appliquer la définition des polygones centrés.
Pour les empilements en pyramide : trois pyramides carrées centrées et quatre racines valent quatre pyramides triangulaires (tétraèdres) centrées et trois racines. D’où l’aboutissement de la démonstration.
En démontrant que trois pyramides pentagonales centrées et quatre racines valent quatre pyramides triangulaires centrées et trois axes, l’auteur prouve ensuite l’identité du dodécaèdre et de l’icosaèdre.
Découvrir et expliquer
Le tétraèdre centré est somme de deux cubes simples, celui de même racine et le précédent. Maurolico en déduit un nouveau cube, assemblage d’un cube et du précédent, le cube « mixte ».
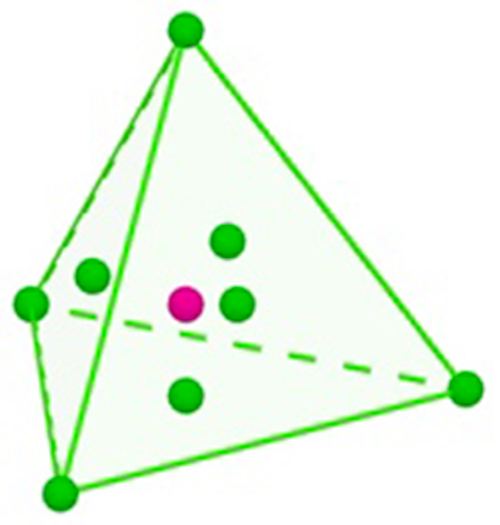
Deuxième tétraèdre centré, 9.
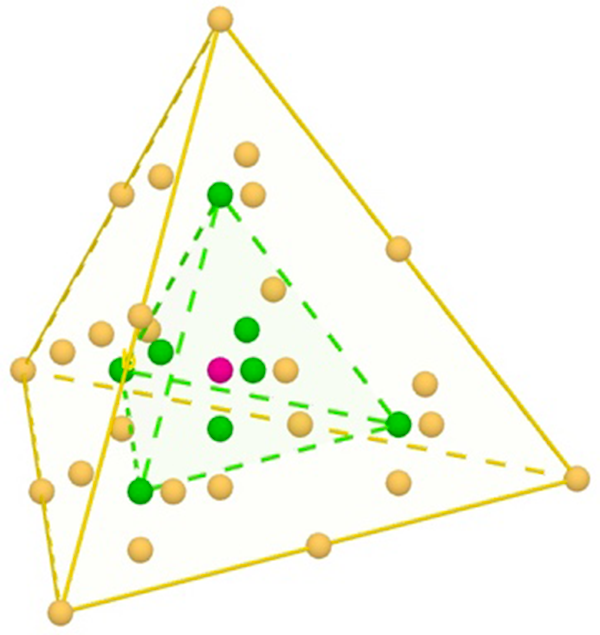
Troisième tétraèdre centré, 35.
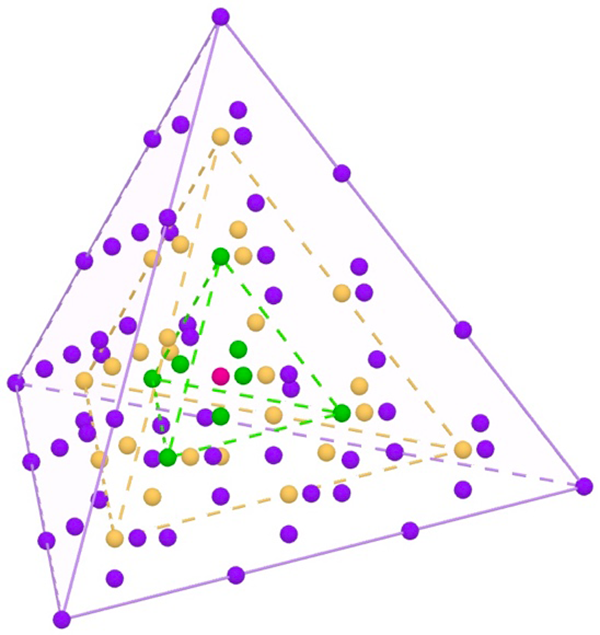
Quatrième tétraèdre centré, 91.
Le cinquième cube mixte, 189, égal au cinquième tétraèdre centré.
« Nous nous efforcerons donc d’expliquer les choses qui nous viennent à l’esprit sur ces formes numériques » écrit Maurolico dans son introduction ; cela va avec le plaisir de convaincre. De fait, l’attention à démontrer marque le projet de l’auteur ; les définitions sont données en termes numériques, les nombres figurés sont des listes de nombres, au-delà de leur acception en termes de figures. On note ainsi divers styles de preuves :
- la référence aux Éléments d’Euclide, avec un emploi « en nombres » pour signifier qu’un énoncé géométrique est exploité en termes numériques ;
- le recours à des schémas, supports de par raisonnement, dont un schéma précurseur du développement du binôme qui justifie des résultats nouveaux, entre autres : les sommes des nombres impairs par paquets de 1, 3, 5… (en nombre impair) sont les cubes centrés, les octaèdres centrés, les pyramides triangulaires centrées de racine impaire ; ces trois nombres solides sont gnomons des bicarrés ; la somme des cubes centrés est le bicarré ;
- le « calcul », tiré de l’expression de nombres figurés en composantes, renforçant le caractère numérique (notamment à propos de l’égalité de certains nombres solides) ;
- le raisonnement sur exemple, fréquent ; en traitant le cas particulier comme porteur de généralité, l’exemple se veut plus que du calcul exemplaire, on réfère aux propriétés qui l’expliquent. Maurolico veille souvent à conclure par une phrase marquant la généralité, sous des formulations dûment variées : « Et de même, dans chaque cas, je montrerai la proposition. »
Par sa démarche pour quelques propositions,
Maurolico fait partie des précurseurs du raisonnement par récurrence, lequel sera le fait de Blaise Pascal (voir notre hors-série 85, qui lui est consacré), dans la treizième conséquence de son Traité du triangle arithmétique (écrit en 1654, publié en 1665).
Cette œuvre arithmétique est bien connue des mathématiciens français du XVIIe siècle. Bachet de Méziriac, dans son Appendice aux Nombres polygones de Diophante, reprend la proposition 62 de Maurolico relative aux sommes de nombres impairs par assemblages de 1, 2, 3…, valant des cubes. Fermat, lecteur de Maurolico, écrira à ce propos une observation marginale remarquable énonçant une propriété plus générale pour les nombres polygones. Il cite (et critique) l’auteur à propos de son étude de la réfraction de la lumière. Pascal a lui aussi étudié Maurolico ; il le cite et utilise ses résultats à propos de ses travaux sur la roulette (la cycloïde) en tant qu’Amos Dettonville ; peut-être y a-t-il eu une influence sur son Traité du triangle arithmétique.
Cette mathématique des nombres figurés, formidablement déployée avec l’œuvre de Maurolico, joue son rôle, en une sorte de point culminant. D’autres modes de représentation des nombres entiers, d’autres questionnements, dont l’étude des équations diophantiennes, vont rapidement surgir et changer le visage de l’arithmétique.
références
•
Le premier livre d’arithmétique de Francesco Maurolycus. Jean Cassinet, Cahiers d’histoire des mathématiques de Toulouse 3, 1981.
•
Francesco Maurolico, le premier livre des Arithmétiques et l’induction mathématique. Jean-Pierre Sutto, Matapli 45, 1996.
•
D’une observation de Fermat à un moment de calcul, Jean Aymès,
APMEP Septembre 2021, Au fil des Maths, n° 541.
•
Édition électronique (en italien) de l’œuvre scientifique de Francesco Maurolico,
par l’université de Pise, années 2000 : http://maurolico.free.fr/intro.htm


