Essayez, à la règle et au compas, de construire un triangle connaissant les longueurs de ses trois côtés. Vous vous heurtez vite à des cas d’impossibilité liés à l’inégalité triangulaire, qui, comme son nom l’indique, constitue une « obligation » dans le triangle. D’autres inégalités peuvent avoir une interprétation géométrique simple ; l’inégalité arithmético-géométrique est l’une d’elles. Certaines, plus compliquées, sont même purement géométriques.
L’inégalité triangulaire
L’inégalité fondamentale du triangle.
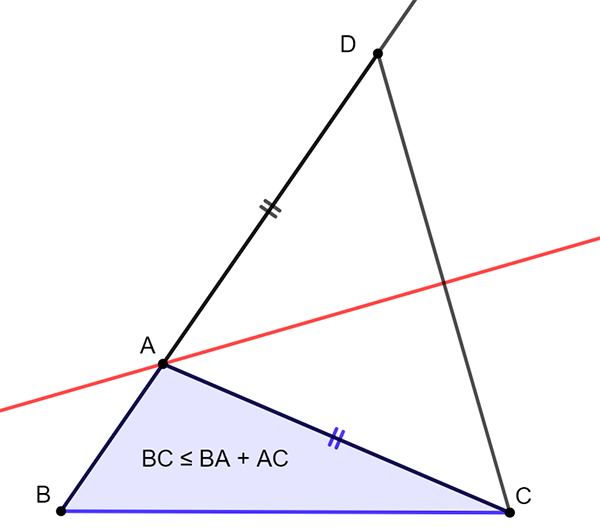
La ligne droite est, dit-on, le plus court chemin d’un point à un autre. Ainsi, dans un triangle ABC, aller de B à C selon le segment [BC] serait plus court qu’en passant par A. Est-ce vrai ?
Considérons le point D de la demi-droite [BA) tel que AD = AC.
B et D étant de part et d’autre de la médiatrice (en rouge) de [CD], B est plus proche de C que de D. Alors BC ≤ BD. C’est dire que BC ≤ BA + AD, soit BC ≤ AB + AC (1). L’adage dit donc vrai ; c’est ce que les mathématiciens appellent l’inégalité triangulaire. En d’autres termes, dans un triangle, la longueur d’un côté est inférieure ou égale à la somme des deux autres. Écrite ici pour une somme, cette inégalité vaut aussi pour une différence puisque, si AB ≤ AC, partant de AC ≤ AB + BC, on obtient, en retranchant AB de part et d’autre, AC – AB ≤ BC, et si AC ≤ AB, à partir de AB ≤ AC + BC, on a finalement AB – AC ≤ BC, d’où l’inégalité |AB – AC| ≤ BC (2).
En jumelant les deux inégalités (1) et (2), il vient |AB – AC| ≤ BC ≤ AB + AC, que l’on traduit en disant que, dans un triangle, la longueur d’un côté est comprise entre la somme et la différence (en valeur absolue) des deux autres.
Inégalités entre moyennes
Diverses moyennes peuvent être définies pour deux nombres a et b :
la plus connue est la moyenne arithmétique,
Viennent ensuite la moyenne géométrique
puis la moyenne harmonique h définie par soit
et enfin la moyenne quadratique (voir l'article « Une histoire de moyennes bien rangées » et En Bref « Encore des moyennes »).
Toutes ont une interprétation géométrique faisant appel à des triangles dans leur construction, et de nombreuses configurations permettent de visualiser leurs positions mutuelles, c’est-à-dire l’ordre dans lequel elles se présentent. Nous retiendrons tout particulièrement la figure de Sidney Kung, qui se trouve en bonne place dans Preuves sans mots de Roger Nelsen (Hermann, 2013).
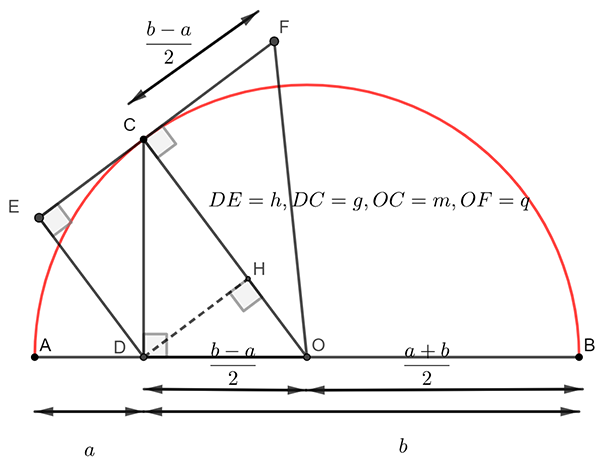
Une preuve sans mots pour classer les moyennes.
Les longs discours sont généralement inutiles pour les « preuves sans mots », mais quelques explications ne seront pas superflues, non pas pour vérifier l’évidence de la figure, mais pour montrer que les moyennes sont bien toutes là.
La figure parle d’elle-même quant à sa construction :
AD = a, DB = b et, O étant milieu de [AB], et
On mène ensuite la perpendiculaire en D à (AB), qui coupe le demi-cercle de diamètre [AB] en C, puis la tangente à ce demi-cercle en C, et ensuite la parallèle à (OC) en D qui coupe cette tangente en E. On place enfin sur la demi-droite [EC) le point F tel que
CF = OD.
Les inégalités, d’abord : elles sont évidentes sur la figure, toutes basées sur le fait que, dans un triangle rectangle, c’est l’hypoténuse le plus grand des côtés. En effet, on a bien, dans le triangle DEC rectangle en E, DE < DC. De même, dans le triangle ODC rectangle en D, DC < OC, puis, toujours dans un triangle rectangle (OCF, cette fois, rectangle en C),
OC < OF, ce qui finalement donne : DE < DC < OC < OF.
Passons maintenant aux liens entre ces quatre longueurs et les nombres a et b, qui donneront en fait les quatre moyennes dont nous avons parlé.
Dans le triangle ABC rectangle en C, DC2 = DA × DB, soit faisant de DC la moyenne géométrique de a et b : DC = g.
Par ailleurs, [OC] est le rayon du demi-cercle de diamètre [AB], donc moyenne arithmétique de a et b.
De plus, dans le triangle OCF rectangle en C, le théorème de Pythagore donne
C’est dire que OF = q, moyenne quadratique de a et b.
Reste maintenant à calculer DE dans le triangle DEC rectangle en E. On a DE2 = DC2 ‒ EC2. Or, EC = DH et DH × OC = DO × DC (le triangle ODC est rectangle en C),
ce qui donne
soit qui est aussi la valeur de EC.
On en vient maintenant au calcul de DE dans le triangle DEC rectangle en E :
d’où
qui fait de cette dernière longueur la moyenne harmonique de a et b.
En définitive, la suite d’inégalités vue plus haut entre les quatre longueurs DE, DC, OC et OF donne exactement h < g < m < q, relation entre les quatre moyennes, harmonique, géométrique, arithmétique et quadratique, qu’une preuve « sans mots » a permis d’établir.
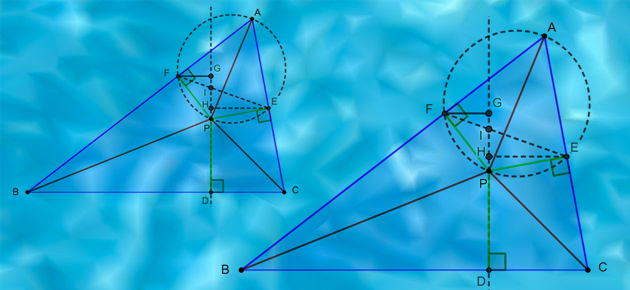
Conjecturée par le célèbre mathématicien hongrois Paul Erdös (1913‒1996), l’inégalité suivante est devenue un théorème après sa démonstration en 1937 à la fois par l’Américano-Britannique Louis Joel Mordell (1888‒1972) et par l’Américain David Francis Barrow (1888‒1970). Le Russo-Américain Nicholas Donat Kazarinoff (1929‒1991) en donna une autre en 1945, qu’il a améliorée en 1957. L’énoncé en est simple : pour un point P intérieur à un triangle ABC, qui se projette orthogonalement en D sur (BC), en E sur (CA), en F sur (AB), on a :
PA + PB + PC ≥ 2(PD + PE + PF).
(inégalité d’Erdős‒Mordell )
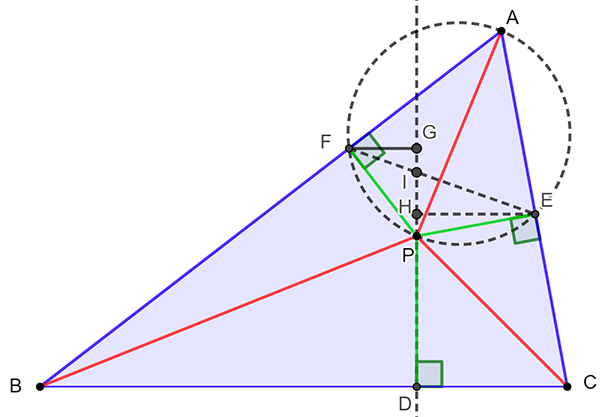
Le théorème d’Erdös‒Mordell.
En voici une démonstration, proche de celle de Mordell. On peut, pour cette preuve, commencer par un lemme :
Pour détailler les éléments de la figure, disons que les points E et F se projettent respectivement en G et H sur la droite (DP), cette dernière coupant (EF) en I. Déjà, les quatre points A, E, F et P sont cocycliques dans le cercle de diamètre [AP], dont on appelle R le rayon.
Dans le triangle AEF, la loi des sinus donne soit
Par ailleurs, le quadrilatère BDPF étant lui aussi inscriptible, est le supplément de
c’est dire que
Ainsi,
ou encore De même,
Or EF, qui est égal à EI + IF, est supérieur ou égal à FH + EG.
On a bien ainsi ce qui démontre le lemme.
Ensuite, en divisant par , il vient :
Puis, par permutation circulaire :
et enfin
On en déduit :
Or, ce qui permet d’écrire cette somme, en appelant Q la moyenne quadratique de
et
et G leur moyenne géométrique, sous la forme 2Q2 / G2. Or, Q ≥ G.
Chacune des sommes entre parenthèses est donc supérieure ou égale à 2. On retrouve bien l’inégalité annoncée : PA + PB + PC ≥ 2(PD + PE + PF).
L’égalité se produit, comme l’a précisé Barrow, dans le cas où le triangle ABC est équilatéral avec P pour centre de son cercle circonscrit (puisqu’alors PA + PB + PC est alors égal au double de la hauteur du triangle, et que PD + PE + PF est exactement cette hauteur). Voilà donc une inégalité inspirée d’autres relations d’inégalités, qui se produisent entre moyennes. Que de liens de parenté entre les inégalités du triangle !