
Les Celtes sont un regroupement de sociétés partageant une identité culturelle commune. Ils peuplent une grande partie de l’Europe, allant des îles britanniques à la péninsule ibérique, et jusqu’en Turquie, pendant une période s’étendant de l’âge du fer à la romanisation en Gaule, et jusqu’au haut Moyen Âge en Irlande et au Royaume-Uni. Ces peuples n’ont laissé que peu de traces écrites, privilégiant une transmission orale de leurs savoirs, et ont développé préférentiellement un art sur des objets utilitaires (céramiques, armes, bijoux), plutôt que sur des monuments comme les Romains et les Grecs.
Leur art se veut intimiste, subtil. Les motifs finement réalisés sont faits pour être vus de près, par les propriétaires des objets qu’ils recouvrent. Les décors obtenus sont stylisés, peu figuratifs, et extrêmement géométriques.
C’est cette géométrie intrinsèque qui permet la création de décors complexes, intriqués, foisonnants, fourmillant de niveaux de lecture et de détails cachés, sans toutefois mettre à mal l’esthétisme général. C’est ici que la géométrisation, l’action de « rendre géométrique », intervient. Les motifs sont organisés selon des principes géométriques poussés, et suivent une logique leur permettant de créer des décors cohérents. Cette géométrisation peut s’étudier par l’ethnomathématique.
Interview de Solène Gallerne

Dans quel domaine de recherche votre thèse s’inscrit-elle ?
J’ai effectué ma thèse à Sorbonne Université, sous la direction de Nathalie Ginoux et Eric Vandendriessche. Mon travail transdisciplinaire regroupe deux champs d’études, l’archéologie et les mathématiques, en mettant en lumière les principes mathématiques et géométriques inhérents aux décors et motifs celtes. Du fait du caractère oral des cultures celtes, et du caractère extérieur de la littérature écrite de la part des Romains et des Grecs nous étant parvenue à leur sujet, je me suis spécialisée en ethnomathématique, ce qui m’a permis d’identifier des idées mathématiques parcourant l’art des Celtes, allant de l’âge du fer continental au haut Moyen Âge insulaire.
Pourquoi avez-vous choisi ce sujet ?
L’étude des cultures passées me passionne, plus encore celles de tradition orale comme les Celtes, qui ont développé un art analogique, à contrario de la tradition naturaliste gréco-romaine. Sous les aspects abstraits et réguliers de l’art des Celtes, se cache un savoir à la fois intellectuel et manuel, afin de créer des motifs chargés de sens et compréhensibles de leurs seules cultures.
Comment cette thèse s’insère-t-elle dans vos projets ?
Je souhaite continuer à étudier les Celtes, je pense que l’avenir de cette discipline repose beaucoup sur la transdisciplinarité et la coopération entre chercheurs. Nous avons ainsi avec Romain Ravignot organisé en 2022 le colloque international « Production des savoirs » rassemblant des chercheurs transdiciplinaires autour de la production du savoir dans les sociétés protohistoriques, et sur l’apport des sciences contemporaines à l’étude de ces sociétés.
Nous avons aussi publié tous les deux en décembre 2023 l’article Représenter le divin chez les Celtes : entre conceptualisation et fragmentation. L’exemple du monnayage à la croix (OMNI n°17, en accès libre sur www.wikimoneda.com/omni), où nous démontrons la géométrisation intrinsèque et symbolique d’une monnaie gauloise, dont le décor est construit selon une triple spirale. J’ai par ailleurs créé en 2021 un blog sur la plateforme Hypothèses devenu par la suite une association, CELTIC (Communauté d’étude et de lecture de travaux internationaux sur les Celtes), que je coanime avec Cindy Cadoret, Dominique Hollard et Romain Ravignot. Depuis un an, cette association permet, lors de séances hebdomadaires, à des chercheurs universitaires et des étudiants celtisants, de venir présenter leurs recherches, d’en débattre entre eux, créant de la visibilité, mais aussi des échanges enrichissants, à la fois pour chacun, mais aussi pour ce champ d’étude.
La constance structurelle
Les décors en bandes décorées sont un bon exemple d’organisation géométrique que l’on retrouve dans l’art des Celtes. Le principe des bandes décorées est explicité par Marcia Ascher dans son livre devenu une référence en ethnomathématique : Mathématiques d’ailleurs (Seuil, 1998). Il s’agit de classer les décors en bandes (ou frises), selon des translations, rotation et symétries du même motif. Il existe sept types d’organisations, dites isométries, que les sociétés celtes maîtrisaient déjà à la perfection à la fin du Hallstatt (premier âge du fer, -650 avant notre ère), notamment sur des céramiques. Les décors en bandes se retrouvent par la suite tout au long de l’âge du fer continental, par exemple sur des fourreaux d’épées, dont la forme se prête bien à ce type de décors, et jusqu’au haut Moyen Âge insulaire dans les manuscrits enluminés. La recherche de l’ensemble des types d’isométries est attestée sur tous ces supports.
Plus que la variété des supports, la persistance de ce type de décors au travers des siècles, des aires géographiques, mais aussi à travers les styles artistiques démontre une constance structurelle inhérente qui met en évidence une pensée mathématique identitaire définissant l’art des Celtes au même titre que le choix des motifs. Un décor en bande décorée de type PMM2 (symétrie verticale et horizontale) peut ainsi se retrouver dans un style « géométrique », composé de formes dites « simples » sur des céramiques, dans un style irlandais foisonnant de micro-motifs végétalisés sur un fourreau d’épée, et dans les entrelacs intriqués des enluminures des manuscrits médiévaux insulaires.
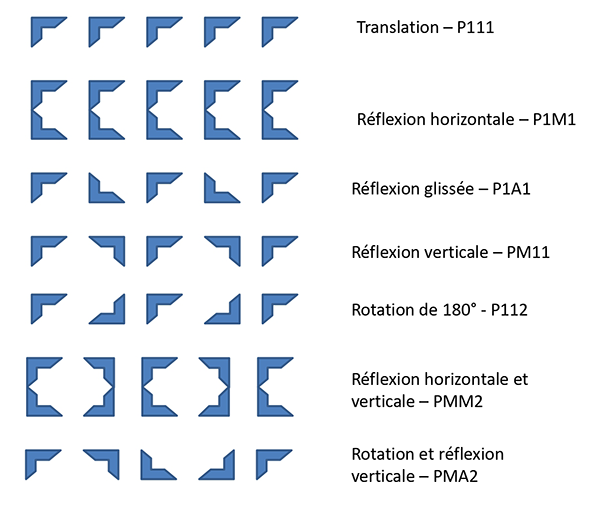
Les isométries dans les bandes décorées celtes.

Livre de Lindisfarne (XVIIIe siècle). Bandes décorées de type P111 (translation simple) dans les frises d’oiseaux et pavages de type P4M (carré totalement symétrique) dans les cadres latéraux de la croix.
Une théorisation a posteriori
Les bandes décorées ne sont pas le seul exemple géométrique pouvant être analysé dans l’art des sociétés celtes. Des principes pythagoriciens ont été relevés sur des phalères (ornements de chars), dont les résilles métalliques évidées minutieusement selon un entrecroisement d’arcs de cercle, démontrent une connaissance et maitrise approfondie du cercle et de ses découpages.

Exemple de travail de découpage du cercle : Phalère de Somme-Bionne.
D’autres principes sont mis en œuvre, comme les pavages. Si d’autres exemples plus tardifs peuvent se rencontrer, comme dans les décors de l’Alhambra en Espagne, le principe même des pavages n’a été théorisé que bien plus tard, notamment par le mathématicien russe Evgraf Stepanovitch Fedorov (1853-1919) qui a démontré leurs déclinaisons en 17 formes à la fin du XIXe siècle, et dont le potentiel artistique a été rendu célèbre au XXe siècle par l’artiste Mauritz Cornelius Escher. Leur présence dans les manuscrits enluminés n’est pas simplement due à un heureux accident artistique, mais témoigne par leur récurrence et diversité d’une véritable recherche par les artistes des formes et possibilités tant à la fois artistique que géométrique qu’offre ce type de décors.
D’autres décors présentent des constructions de type fractal (elles aussi théorisées au XXe siècle), répétant des motifs dans les limites physiques imposées par le support. Que ce soient les bandes décorées, les pavages, ou les fractales, les constructions géométriques celtes démontrent une volonté d’affranchissement du support, d’exister au-delà de ce que l’œil humain peut percevoir.
La recherche du mouvement
L’art des Celtes frappe au premier regard par son impression de dynamisme, de vitalité, se dégageant des compositions pourtant majoritairement non figuratives. Cet effet est non seulement obtenu par l’affranchissement des périmètres du support, mais aussi par la recherche de profondeur, grâce à des jeux de perception, de double lecture, entre le motif et son arrière plan. Le support des motifs, l’objet en tant que tel, devient un élément clé de son propre décor, notamment sur les miroirs, dont la forme même est une mise en abyme de type fractale, et dont les motifs remplissant cette forme offrent un jeu entre ceux dessinés au premier plan, et ceux se découpant à l’arrière plan. Plus encore, ces deux types de motifs se répètent à différentes échelles, et sont remplis d’une figuration cachée, présentant des têtes d’oiseaux.
Miroir de Desborough (Grande-Bretagne ;
Ier siècle avant J.-C. − Ier siècle après J.-C.).
Jeux de double lecture, de lumière, et de fractales entre les motifs et l’arrière plan.
Cette double lecture se retrouve de même dans toutes les compositions, où elles peuvent dupliquer un second type de bande décorée en arrière-plan d’une frise, présenter des compositions triangulaires entre les arcs de cercle des phalères, et offrir un répertoire de formes plus étendu dans les miroirs.
Cette combinaison de principes mathématiques et géométriques participe donc à une impression de profondeur, et de mouvement, dont les entrelacs des manuscrits reprennent le principe. Les brins formant les entrelacs, passant une fois au dessus, une fois en dessous les uns des autres, démontre une recherche de relief et de profondeur, une conquête de la troisième dimension, tout en créant une rythmique par la répétitivité du motif, inspirant une possibilité de continuité au-delà des frontières imposées par l’objet.
Les maîtres du savoir
Ces productions artistiques semblent attester d’une connaissance approfondie des principes mathématiques et géométriques mis en œuvre. En effet, les formes et motifs obtenus ne sont pas le fruit du hasard mais le résultat d’un raisonnement, considérant les principes mécaniques de l’objet support, les limites de la surface allouée au décor, mais aussi leur symbolique intrinsèque, et l’effet souhaité sur l’observateur. Cela pose la question de l’accès à une forme d’éducation mathématique et géométrique.
La répétitivité des motifs obtenus dans les bandes décorées ou les pavages des manuscrits, ce que Mary Carruthers nomme « composition mémorative » dans son ouvrage Le livre de la mémoire (Macula, 2018), favorise par son agencement rythmique un état mental propice à la mémorisation des textes sacrés associés aux enluminures. Le jeu de double lecture traduit quant à lui un affranchissement du support, et sur les miroirs, permet un jeu de lumière avec la surface métallique, donnant de plus un aspect vivant à ces motifs.
Les phalères étaient disposées sur des chars et harnachements de chevaux, les fourreaux et les céramiques étaient manipulées, les pages des manuscrits tournées. Ces décors, par leurs multiples niveaux de lecture et de points de vues, traduisent donc une prise en compte de leur utilisation et de leur examen sous plusieurs angles. Ils prennent ainsi vie entre les mains de leur observateur, une vie régie par des principes mathématiques et géométriques, et habillée par des répertoires de formes complexes.

