
«Un bon croquis vaut mieux qu’un long discours » disait déjà Napoléon. C’est vrai aussi en mathématiques où cependant figures, dessins et diagrammes ont été longtemps bannis des ouvrages « sérieux »… et même des ouvrages de géométrie. On est aujourd’hui revenu à une prise en compte de tout l’aspect visuel que peut revêtir une démonstration, de tout ce qu’un diagramme peut aider à développer d’intuition pour que, d’un seul regard, la lumière se fasse et qu’on se dise : « Bon sang, mais c’est bien sûr ! » Alors, même si « montrer n’est pas démontrer », dessins et diagrammes permettront peut-être, à défaut de bâtir une argumentation, au moins de trouver une voie qui y mène. Revenons ici sur ces preuves sans mots qui aideront grandement à visualiser des situations pas toujours géométriques en apparence ou des propriétés parfois insoupçonnables.
Des formes mais pas de mots
Lorsqu’on pense « figures », on pense évidemment « géométrie », et s’il est un domaine où se sont le mieux développées les preuves sans mots, c’est bien celui-là. Un manuscrit chinois datant de deux cents années avant notre ère en donne déjà un exemple, rendant évident le célèbre théorème de Pythagore (voir Tangente 172, 2016).
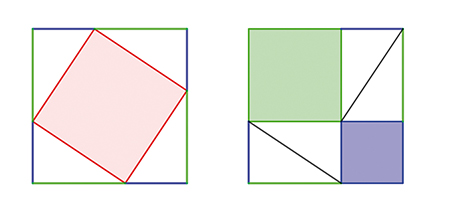
Pythagore sans rien dire.
D’un seul ... Lire la suite
