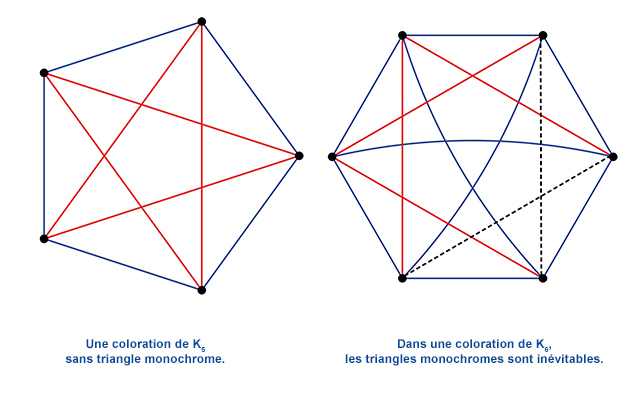
Considérez n points et reliez-les tous les uns aux autres par des arêtes de deux couleurs au choix (bleu ou rouge). Vous venez de dessiner une 2-coloration du graphe complet Kn . Avec cinq points, il est possible de choisir les couleurs de façon à ce qu’aucun triangle ne soit d’une seule couleur. En revanche, dans K6 , il est inévitable d’avoir un triangle monochrome. En effet, cinq arêtes partent du sommet A et comme il n’y a que deux couleurs possibles, trois d’entre elles, [AB], [AC] et [AD] par exemple, sont de la même couleur (mettons bleu). Si BCD n’est pas monochrome, alors au moins l’un de ses trois côtés est bleu et forme donc un triangle monochrome avec A.
Ces petits problèmes amusants ont été étudiés à la fin des années 1920 par le Britannique Frank Plumpton Ramsey (1903–1930). La question se généralise ainsi : quel est le plus petit entier R(n) tel que toute 2-coloration de KR(n) contienne forcément un sous-graphe Kn monochrome ?
On a R(3) = 6. En 1955, il a été établi que R(4) = 18 : dans toute 2-coloration de K18, il existe un sous-graphe complet d’ordre 4 monochrome, mais ce n’est pas le cas pour K17.
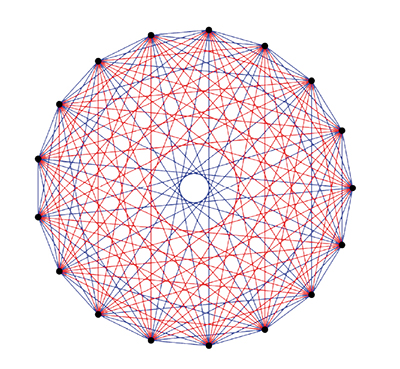
Une 2-coloration de K17 dans laquelle aucun sous-graphe complet d’ordre 4
n’est monochrome. Si l’on note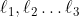 
les huit longueurs d’arête possibles,
on a colorié en bleu les arêtes de longueur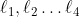 
et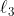 
et en rouge les autres.
Pour les valeurs suivantes, seuls quelques encadrements sont connus : R(5) est compris entre 43 et 49, et des travaux récents tendent à confirmer la borne inférieure. Pour R(10), la valeur est comprise entre 798 et 23 556.