
Avec n = 3 segments, on peut dessiner un triangle. Avec n = 4, combien peut-on dessiner de triangles distincts (qui ne se superposent pas) ? La réponse est 2. Les problèmes arrivent vite lorsque n augmente ! Énoncée en 1978 par le mathématicien japonais Kobon Fujimura (voir Tangente SUP 46, 2008), la question a été popularisée par Martin Gardner, expert incontournable des mathématiques récréatives, en 1983.
Saburo Tamura a démontré peu après que le nombre maximum de triangles formés par n segments est majoré par la partie entière de
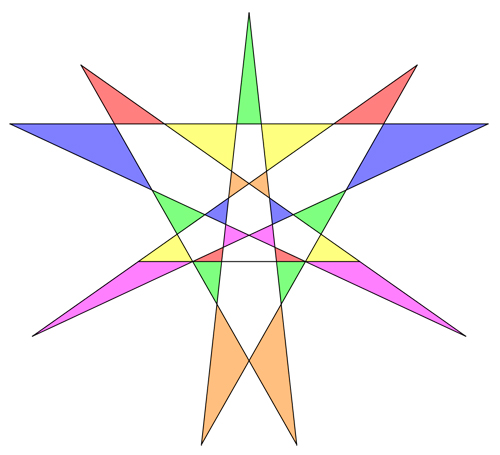
Vingt-cinq triangles pour dix segments. Arriverez-vous à faire mieux ?
D’autres mathématiciens ont démontré plus récemment que cette borne ne peut pas être atteinte si n est un multiple de 6 ou la somme d’un multiple de 6 et de 2. Les résultats optimaux sont connus jusqu’à n = 9 mais dès n = 10 des incertitudes demeurent : peut-on obtenir vingt-six triangles ? De quoi occuper vos longues soirées d’hiver !
