
Les observations synthétiques connues à l’époque de Newton sont essentiellement les trois lois de Kepler, obtenues de façon empirique au début du XVIIe siècle mais très bien testée sur les planètes. La première loi affirme que la trajectoire des planètes est une ellipse dont le foyer est occupé par le Soleil. La deuxième loi avance que l’aire du parallélogramme engendré par les vecteurs position et vitesse (pour le formuler dans un langage moderne) est constante. Enfin, la troisième loi stipule que le carré de la période est proportionnel au cube de la plus grande longueur de l’ellipse.

Pour tenter d’en rendre compte, Isaac Newton (1642–1727) propose deux axiomes intriqués, qui posent les bases d’une méthode mathématique pour la résolution des problèmes physiques :
1) Un corps isolé est en mouvement rectiligne uniforme : sa vitesse ne varie pas dans le temps, et donc, à cette vitesse constante près, son mouvement « est comme rien » ; c’était une remarque de Galilée, un contemporain de Kepler…
2) Par contraposée, si la vitesse d’un corps varie dans le temps, c’est qu’il est soumis à l’influence d’une action dont c’est la caractéristique : une force. C’est là une sorte de définition de la notion de force, et la fameuse équation de Newton relie dans les cas « simples » la somme des forces appliquées à un corps, de masse m, à la variation temporelle de sa vitesse
. On écrit :
Expérimentalement, il était nécessaire d’introduire cette masse m. Elle permet, en appliquant une même force, d’avoir un effet variable sur la vitesse (pensez à l’action d’une même force sur un moustique et sur un train de banlieue…).
La géométrie des Anciens
En plus de doter la physique d’un outil d’investigation, la définition de Newton permet de se poser des questions en contemplant la nature, et parfois même d’y répondre. C’est donc en observant ou en pensant la chute de divers corps que le savant britannique postula la gravitation. Le raisonnement est élémentaire. Une pomme attachée à son pommier est immobile. D’un coup, elle tombe. Sa vitesse avant de se décrocher de l’arbre était nulle. Puis on la voit accélérer, jusqu’à s’arrêter brutalement en touchant le sol. Dans cette aventure, la vitesse de la pomme a varié ; c’est donc que la pomme est soumise à une force. L’effet de cette force au niveau de la surface de la Terre est de faire parcourir cinq mètres à une pomme en une seconde ; vérifiez-le !
Pour la Lune, c’est en fait un peu la même chose. Imaginez que la vitesse de la Lune ne varie pas (au moins en direction) ; comment pourrait-elle rester en orbite autour de la Terre ?
Si la Lune allait tout droit, sans subir aucune force, en une seconde elle serait au point P du schéma (qui n’est évidemment pas à l’échelle). Mais en fait, à cause de la force qu’exerce sur elle la Terre, elle se trouve au point Q. La hauteur de chute est donc la distance PQ. Depuis l’Antiquité, on sait que l’orbite de la Lune est « quasiment circulaire » et uniforme, la vitesse de la Lune en M est donc tangente au cercle orbital, et ainsi perpendiculaire au segment [OM]. Le vecteur contenu dans la droite engendrée par cette vitesse est donc perpendiculaire au vecteur
. Ainsi, le triangle OMP est rectangle en M.

Par ailleurs, la Lune revient à peu près au même endroit dans le ciel tous les vingt-huit jours, et depuis l’Antiquité (avec Aristarque de Samos) on avait déterminé, par des mesures de parallaxe, que la Lune se situait à soixante rayons terrestres de la Terre. Le rayon terrestre avait lui aussi été déterminé par les Grecs (avec Ératosthène de Cyrène), il vaut R T = 6 400 km. On peut donc calculer la norme de la vitesse de la Lune : notre satellite parcourt un cercle dont on peut déterminer la circonférence en vingt-huit jours ; on trouve :
v = 2π x 60 x 6 400 / (28 x 24 x 3 600) = 1 km / s,
un kilomètre par seconde. Ce résultat numérique merveilleux nous fournit la norme du vecteur , qui mesure donc 1 km.
Ainsi, dans le triangle rectangle OMP, on connaît les longueurs MP et OM. Le théorème de Pythagore nous donne alors (OQ + QP)2 = OM2 + MP2. Sachant que, sur l’orbite circulaire, OQ = OM, on peut résoudre une équation du second degré pour trouver QP = 1,3 mm. Chaque seconde, la Lune tombe d’un peu plus d’un millimètre pour rester en orbite circulaire autour de la Terre…
Vers une loi universelle
L’affaire prend une autre envergure lorsque Newton propose que la force qui fait tomber la pomme est la même que celle qui fait tomber la Lune, et que cette force ne dépend que de la distance au centre de la Terre : les pommes du Lincolnshire, comme celles d’Australie, et tout comme la Lune, se déplacent en direction du centre de la Terre… Cette force serait donc universelle, mais comment dépend-elle de la distance au centre de la Terre ? Pour le savoir, il suffit de comparer ses effets : la pomme, située à un rayon terrestre du centre de la Terre, tombe de cinq mètres en une seconde. La Lune, située soixante fois plus loin, ne tombe que de 1,3 mm, soit 5 / 60 2.
Il n’en faut pas plus pour que Newton propose que cette force de gravitation universelle dépende de l’inverse du carré de la distance. Le reste est une affaire d’unités : il faut que l’expression de cette force dépende des deux masses et que si l’une de ces deux masses est nulle la force soit nulle. Sans masse, il n’y a pas de gravitation chez Newton… Le plus simple, intuitivement, est d’introduire le produit de ces deux masses au numérateur de la norme de cette force.
Il faut ensuite ajuster cette norme aux effets observés et faire en sorte que les unités de la formule obtenue soient celles d’une force, c’est-à-dire celles d’une masse multipliée par une accélération. Newton est donc conduit à introduire ce que l’on appelle, en physique, une constante fondamentale, qui règle ce genre de problème.
Il fixe G = 6,67.10 –11 m3 kg–1 s2.
Il obtient donc
ou encore
Cette formule donne l’expression de la force de gravitation avec laquelle le corps de masse M attire celui de masse m, ces deux masses étant supposées ponctuelles et séparées d’une distance r.
Le vecteur est de norme 1, dirigé de M vers m (ce qui explique le signe, car
attire m vers M) : il sert à bien définir la direction et le sens de la force. La constante de gravitation G sert à « rétablir » les choses.
Les puristes auront remarqué que, avec Newton, on a fait l’hypothèse que les deux masses étaient ponctuelles et que l’action réciproque de m sur M ne faisait pas varier la vitesse de M. En d’autres termes, M est « très supérieure » à m, ce qui est bien le cas du Soleil par rapport aux planètes…
L’introduction des fluxions
Le fait que soit dirigé en permanence par
permet également de montrer que le vecteur orthogonal à
et
et de norme égale à l’aire du parallélogramme formé par ces deux vecteurs est constant. Ce vecteur
n’évolue pas dans le temps alors que
et
varient. C’est la deuxième loi de Kepler.
La difficulté du problème posé par Newton réside en partie dans le fait que le vecteur unitaire dirigeant l’axe (Mm) varie au cours du temps. En effet, si M peut être supposé fixe, ce n’est pas le cas de m, qui subit l’influence gravitationnelle du corps lourd : la distance r est une fonction du temps, le vecteur
ne change pas de norme car il reste unitaire mais il change de direction en suivant la masse m au gré de son mouvement.
Pour résoudre le défi du mouvement de la Terre autour du Soleil, Newton commence par un peu de calcul différentiel, ou théorie des fluxions, comme il disait. Choisissons un système de référence fixe dans lequel on va pouvoir décomposer simplement le vecteur unitaire
; c’est un repère cartésien (pour les mathématiciens) ou galiléen (pour les physiciens). On le prend orthonormé. Faisons un schéma dans le plan contenant le mouvement.

On a La variabilité temporelle de
est ainsi transportée dans celle de θ = θ (t), mais les vecteurs unitaires
et
sont désormais fixes.
Faisons varier par rapport au temps :
Le vecteur est donc également unitaire ; il correspond à
« tourné » de π/2 radians :
Le repère est donc orthonormé ; on le nomme repère polaire local (il est « local » car il faut le reconstruire à chaque instant). En dérivant
par rapport au temps, la rotation continue :
, soit encore
.
En reportant dans le principe fondamental de la dynamique, il vient :
En écrivant et
dans cette base polaire locale, un simple calcul montre que l’aire Λ du parallélogramme qu’ils forment à chaque instant s’écrit Λ = r 2 dθ / dt. Ainsi, le vecteur
possède une norme constante.
Finalement, grâce à tous ces miracles, le principe fondamental de la dynamique se résume pour ce problème en
, soit encore
Le vecteur de Hamilton est donc constant ! Et il est dans le plan du mouvement.
Caractérisation de l’orbite
Pour caractériser l’orbite de m autour de M, Newton n’utilisait que des figures. Suivons son raisonnement, en utilisant un outil plus moderne : le produit scalaire (voir Vecteurs et Espaces vectoriels, Bibliothèque Tangente 65, 2018).
Le produit scalaire des vecteurs et
est défini par
En remplaçant par sa valeur, on obtient
Or, le vecteur est porté par la direction de
Ainsi,
d’où
et enfin
On en déduit l’égalité .
En utilisant et en choisissant l’origine des angles telle que
il vient la relation fondamentale :
avec
et
.
Nous sommes au bout de nos peines ! Cette relation entre r et θ est la définition d’une conique de paramètre focal p et d’excentricité e (voir l’Unification des coniques, Tangente 162, 2015 et Propos elliptiques, Tangente 163, 2015). Newton a résolu le problème posé sans résoudre aucune équation différentielle et en ne faisant pratiquement que de la géométrie ! Les ellipses de Kepler ont trouvé leur explication par une déduction logique basée sur l’axiome de la définition de la force appliquée au cas de la gravitation.
À la règle et au compas…
Les amateurs de géométrie souhaiteront pouvoir tracer point par point, à la règle et au compas, la trajectoire obtenue en partant de la donnée de la position et de la vitesse à un instant t. Il faut pour cela construire le lieu des vitesses…
À chaque instant, le vecteur vitesse s’écrit . En notant ? x et ? y les coordonnées cartésiennes du vecteur constant
et en exploitant l’expression obtenue de
à chaque instant t, on obtient :
Le lieu H des vecteurs vitesses paramétrés par le temps (ou hodographe) est ainsi contenu dans un cercle de rayon u et dont le centre est pointé par le vecteur . L’hodographe H sera tout le cercle si θ (t) parcourt tout le segment [0, 2π], ou seulement un arc de ce cercle sinon. Dans le cas des orbites périodiques des planètes autour du Soleil, l’hodographe est évidemment le cercle complet…
On peut même préciser tout cela en fonction de l’excentricité e de la conique obtenue. On peut également toujours choisir des unités physiques telles que et donc
.
L’hodographe peut être construit uniquement à la règle et au compas. Sur le schéma ci-contre, l’origine des vitesses est le point M origine du repère cartésien ; représente la vitesse, supposée connue, du point m à l’instant t.
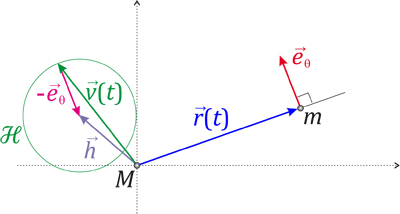
Commençons par mesurer Λ, l’aire du parallélogramme formé par la position et la vitesse à l’instant t. On projette orthogonalement en B le vecteur position sur la droite
engendrée par le vecteur vitesse.
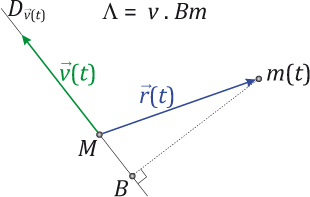
Pour chaque nouveau point de la trajectoire, correspondant à un instant t’, on procédera en trois étapes. Admettons que l’hodographe H soit tout le cercle (orbite périodique). En choisissant un autre point sur H, on construit un nouveau vecteur vitesse . Le vecteur de Hamilton, constant, permet alors de construire
. En faisant tourner ce vecteur de –π/2, on obtient le vecteur unitaire
, qui donne la direction de la droite
.
La droite contient la masse m à l’instant t’ ; comment déterminer sa position ? Il suffit d’utiliser le fait que l’aire Λ du parallélogramme formé par la position et la vitesse n’a pas changé ! En déplaçant m(t’) sur la droite
, sa projection orthogonale B sur
varie également.
Enfin, dès que , on a trouvé le vecteur
.
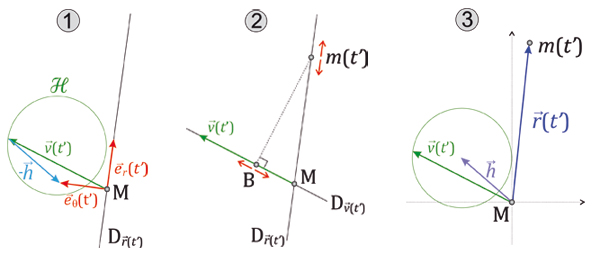
On relance cet algorithme géométrique pour toute autre vitesse. Ainsi, comme toutes ces constructions sont réalisables à la règle et au compas, on peut tracer l’orbite point par point !
