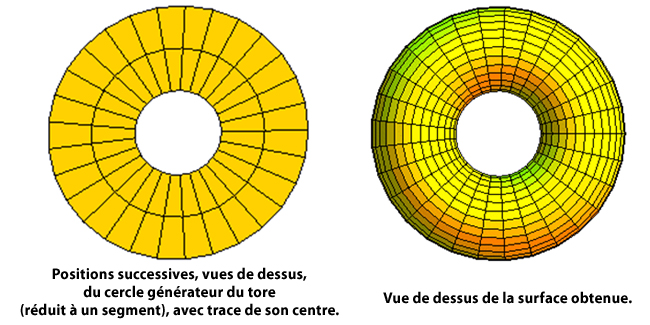
Les figures emblématiques de la géométrie dans l’espace sont la sphère, les surfaces de révolution… dont le tore, ce beignet en forme de bouée ou de chambre à air. Pour cette surface, la vue de dessus du cercle générateur donne donc une couronne.

Prenons maintenant un cercle générateur dont le centre décrit toujours un cercle, mais qui reste parallèle à lui même, dans un plan perpendiculaire au cercle des centres. La vue de dessus des positions successives du cercle générateur et la vue de la surface donnent maintenant ceci : 

La surface obtenue

s’appelle

un dôme de Bohème.

Les surfaces de translation

Cette surface est une réunion de cercles translatés les uns des autres. il s’agit d’une surface dite de translation : c’est ainsi que l’on qualifie la surface engendrée par une courbe A qui reste dans un plan parallèle à lui-même ; un point de ce plan décrit une courbe B. C’est donc une surface résultant de la translation d’une courbe (première génératrice) le long d’une autre (deuxième génératrice) ; cette définition est symétrique en ce sens que la translation de la deuxième génératrice le long de la première donne la même surface. Ceci est illustré sur ... Lire la suite