
L’idée de base de la géométrie descriptive est d’utiliser deux plans de projection orthogonaux : le plan frontal et le plan horizontal. Un point M de l’espace est caractérisé par ses deux projections orthogonales : m (en rouge) sur le plan horizontal et m’ (en vert) sur le plan frontal. On rabat ensuite les deux plans de projections l’un sur l’autre afin de les représenter ensemble sur une même feuille, l’épure du point M.
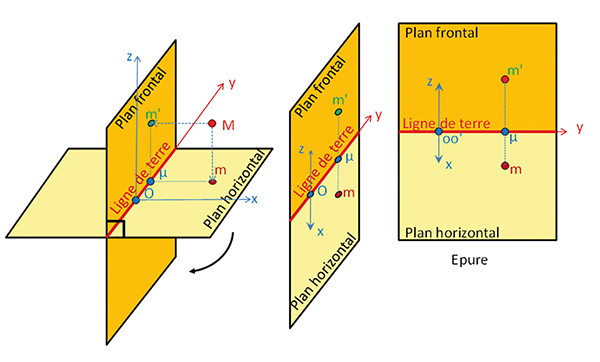
Ainsi, sur l’épure figure la ligne de terre, intersection des deux plans de projection, charnière du rabattement de nos deux plans. Chaque point se trouve représenté par ses deux projections, reliées par une droite appelée ligne de rappel, perpendiculaire à la ligne de terre. Par convention, on énonce d’abord les projections horizontales, et ensuite les projections frontales, qui sont « primées ». Ainsi, le point M est représenté par (m, m’). Les points m et m’ se projettent en μ sur la ligne de terre. Tous les points de l’espace peuvent ainsi être représentés de façon non ambiguë.
La valeur algébrique est l’éloignement du point M (sous-entendu « l’éloignement du plan frontal ») et la valeur algébrique est la cote du point M. Sur les épures, on ne représente pas ... Lire la suite
